Advanced Prehistoric Science

Index Page

Exact Reconstruction of Petrie's Giza Ground Plan

The Layout of Giza's Pyramids is a minimum of 15,000 years old

Testing the Nazca Monkey for Connections to the Great Pyramid

A Long Atlantean Message in Thirteen Numbers - The Frame

The Frame - the Hex-Machine - a family of three hexagons

Abydos Helicopter & the Golden Section

Hesire's Tomb Door

Giza Pyramid Temples & the Golden Section

Next - Nazca Monkey Report

The Athena-engraving & Advanced Prehistoric Science

this image may be the most important work of advanced prehistoric science in establishing rapport to this time

this image may be the most important work of advanced prehistoric science in establishing rapport to this time


In the beginning I was thrilled by fantastic imagery percolating from my subliminal perception. For instance, lines inside the lady's torso made me think of the Giza pyramids; and the torso itself looked like a flying saucer with a cupola on top. In fact, the entire image could be disassembled into what looked like Hi-tech craft. Could it be that this image held secrets of prehistoric pyramids, civilisation, even Aliens? To my chagrin, when I tried to share my impressions with friends, they found them amusing, but off the wall. What was a vivid visual testimony to me, was trivial to them. Were the Ancients just teasing, mocking from the shadows? That could be a sign of their malevolence. On the other hand, if these Ancients were nice, they might furnish the proof by formal design. Thus was born my initial hypothesis - an assumption based upon ethics.

Discovering Geometrical Elements in the Athena Engraving


Late summer, 1985 _ after weeks of admiring the mysterious Stone-Age engraving, I put it to the test for geometrical ideas. I wanted to verify my impression that the torso of the human figure was like a regular lens, an overlapping area of two circles of the same size. I saw some points (crossing lines), where I felt the circle centers might be. I also saw a point, where the arcs might meet, if extended past the line slicing the lens off (the circled point on the right). Check-points Using a pair of compasses, I experimented with a circle from each point to see how well it would mesh with the contours of the torso. From the result we see that in order to confirm that lines stay on course, the engraving establishes virtual check-points : both arcs run either with, or within the short lines of the torso or thread themselves through breaks in the lines of the torso or limit other lines or pass through points (line crossings) * Altogether, there are 25 instances of the circle arcs coinciding with the torso, out of which only three seem random. The Diamond Square The centers of the torso circles, and the points where the circles intersect - mark out four corners of a square, all in thee black. The square is oriented like a diamond and its diagonals form a cross. The lines and extended diagonals of this square coincide with the engraving rather ostensibly. Onwards, its name will simply be the Square. It is the second most important geometric figure in the engraving, and we shall witness its reincarnation in the monkey figure from Nazca.


Moving Parts The regular lens, which we have established on the torso, can be shifted a little to a new snug fit with the torso, shown in the diagram below. This fit is simply faultless. Each arc of the lens passes entirely within one of the two long engraved arcs of the torso. Evidently, the lens has moved, and rotated - so, some mysterious dynamics are at play, here. Of course, a question can be asked if this second torso lens did not actually come first. It did not. The precedence of the first torso lens is firmly established by the rest of this report .


Below: The yellow circle is the Square's circumcircle. The purple circle is identical to the blue torso circles; its radius equals one side of the Square. Both circles pass a number of check-points; they join arcs and touch points on their passage through the engraving. The rose space between the circles contains engraved lines which seem to be split into two halves which rotate against each other. Coloring makes the lens in the middle stand out sharply. The psychological effect of protracted staring at the lens may be three-dinensional apparitions of pyramids within.

The K-Circle


The top corner of the Square rests on a marked point (crossed lines) on a beautifully engraved arc. This 'random scribble', as many an expert on prehistoric art would say, is visibly symmetrical with an arc of the girl's hat. This case is a great example of the art's technical perfection (the magnification below). The free floating arc is especially strong. The two arcs are: 1) concentric 2) symmetrical through their common centre 3) lay on the same circle That's three notable orderly facts. The circle implied by the two arcs is onwards called the K-circle. The K-circle plays a key role in the system. Here, the K-circle is seen passsing through two big points on the Square - the top corner and the center. Looked at closely, this passage is slightly inaccurate. The overall idea suggests exact design, as in the image above; I was given to pondering whether one or the other element, or both, had moved.

The answer to the dilemma is found in the exact geometric blueprint, in which the Square along with everything else owes its existence to the Mother-star. Superposition of the design over the engraving shows almost everything corresponding to that original position, but not the star itself. The star had moved.

Movement

The concept of a moving star is acceptable; stars move, but many would scoff at the idea of moving pyramids; the great pyramids are the antithesis of mobility.
In the plan of this engraving, however, the three Giza pyramids do move, as does mostly everything else, it seems. The plan takes care of all the logistics: it prepares the alternate home bases and the road to get there, as you will see.

Some arcs in the engraving seem so perfectly circular, one starts wondering about what tools were used. The arcs are like sockets inviting placement of corresponding circles. That was the step I took after discovering the Square and the K-circle.

A group of six circles in the above image seems to adhere to one standard size.

The Hip-lens

The below diagram is a considerably blown up scan of an old experiment of mine on paper with a pair of compasses. It revealed another fine example of the engraving's technical excellence. Both arcs of the hip-lens, one long and one short, have the same radius. The corresponding circles have a line of centers which is one and the same with the line of centers K-circle - Square.

The idea is, of course, pure geometry _ and a most noteworthy fact, for a Stone Age artwork is turning out to be the All Time Greatest in precise implementation of exact abstract ideas.

There is more order _ the below diagram shows how the Hip-lens is clearly defined by the K-circle and the Square; it is reconstructible:

The big circle in the diagram, drawn from the bottom corner of the Square, does more than co-create the Torso-lens; it is a triple factor in the creation of the Hip-lens.

1) a line from its center, perpendicular to the line of centers K-circle_Square, gives the center of one of the two circles creating the Hip-lens.

2) the diameter of that Hip-lens circle is then set by the intersections of this big circle with the K-circle_Square line of centers.

3) yet another perpendicular to the line of centers, this time from the bottom of the big circle, is the same as the long axis of the Hip-lens.

Having delineated half the Hip-lens, its completion is easy.

Having an exact idea in one's mind is one thing; transfering it to a medium is quite another. It requires technique, and any technique bases on some technology, whether it be a primitive flint engraving tool or a laser beam.

The transfer of exact design upon stone, as shown below, is of sufficiently high quality to rule out usage of primitive tools in primitive environment.

A cluster of five same-size circles rises from the Hip-lens _ all coming from arcs on Athena's right leg. By the way, these circles are significant in that they are standard on the most important 5-pointed star in the engraving (discussed later).

Vesica Pisces _ The top two circles center on each other, implying the diamond shape composed of two equilateral triangles. Two parallel sides of the diamond imitate lines 'a' and 'b'. Their common axis (green) then does a fabulous passage through the engraving, which needs no detailed description since the mutual order is so blatantly evident.

All these circles in the cluster are good at following edges of their seminal arcs.

Equilateral Triangles.

The left side of the top triangle runs practically parallel some ¹/₁₀₀₀ of a unit (0.02 millimeter) away from the line of centers 'a'.
Line 'b', the long axis of the Hip-lens, is also very close to a side of the lower triangle, but it is 'a' which looks perfect.

My rule is to always experiment with what the engraving seems to suggest, On this occasion, I let line 'a' set one side of the diamond. The top of the diamond goes where 'a' touches the engraved line at the top.
This step had adjusted the position of the circles slightly, and I noted that it meant an improvement, the best looking result.

Of course, things are not always clear cut; the position also suggests that the diamond should possibly be an exact fit between 'a' and 'b'. This doesn't work, however, for the resulting circles do not fit the arcs nearly as well.

So,, why the dual suggestion? In the first variation, the circle radus is 1.00405708.. unit; in the second, it is 0.9960499 unit.
The average then is 1.00006 unit - ⁶/_100,000off an even unit. There may be something to this, after all.

A Constructionist Masterpiece

We have only just begun the engraving's analysis, and it already presents evidence of erudite planning any modern artist could be proud of. We see a system of aligned lenses (each arc of the K-circle also qualifies as a lens since it focuses on the center point between the two). Potentially, K-circle's arcs could be meant to rotate around their common center, while the Hip-lens and the K-circle could rotate around the Square's center.

Next, along with other things, we'll learn how to recreate the K-circle, needed to recreate the preceding diagrams from scratch, and how to determine the engraving's units of length.

Discovering the Mother Star - the Cone

The Cone had emerged from the complexity of the engraving after I had covered it by a multitude of circles based upon arcs. Among all those, two sizes seemed repetitive.

When a given arc indicates a circle, that circle is not sharply defined. Rather, it has a narrow range of possibilities, which all look just about as good, as they all seem to follow the arc.

Can we determine what circle is the intended one for a given arc?

Such a circle should fit nicely not only the arc, but also elsewhere in its area, and, conceivably, an idea suggested by the position:

Is the circle's center signalled by a marked point (crossed lines) in the engraving?
Does the center lay on a line edge (the preferred location)?
Is the circle propped against other lines, and line ends?
Does it pass through points like line crossings with some frequency?
Does it look the same size as a number of other circles?

Compliance with the above criteria suggests that it is the intended circle.

Engraved arcs translate into three symmetrical circles which set the Magic Cone puzzle

The K-circle takes part in the balanced layout of Athena from head to toe, as we just saw. One of its tricks is forming a line of centers with the Square and the Hip-lens. Now it does the same with two more circles and adds the magic of symmetry. The result is the Cone (diag. above).

The Cone & Square formation

The Cone is a fully-fledged geometrical figure that is already connected to the Square by an exact relationship (as shown below). Cone's appearance strengthens the artificiality of the overall position and magnifies its mystery.

Further progress came from the observation that the Cone duplicates the tip of a 5-pointed star; therefore, it may have had its origin in such a star.

Does the Cone carry instructions on how to reconstitute that star?

The Breakthrough

Quite a few arcs in the engraving of Athena translate into circles much like the Cone's middle circle. Based on this frequency of appearance, the Cone's middle circle could conceivably be a unit circle.

Therefore, measuring the Cone by this circle is natural.

step by step:

Surprise # 1

I drew unit(?) circles spaced by the radius along each arm of the Cone. The circles centered three radii in from the tip of the Cone intersected dead in the center of the middle circle. The middle circle had become reconstructible.

Spectacular result - a double revelation!

Cone Mapping diag.

Surprise # 2

Next, I saw that five such radii are just a little short of covering the Cone's sides entirely; however, the same mapping circle, when drawn concentric with the Key-circle, becomes a perfect capping circle for the formation since it is tangent to the two nearest circles on the Cone's sides.

So, in reverse, if we conclude the process of mapping the Cone with the unit-circle capping the formation, the center of the capping-circle will be the K-circle's center. Now we can reconstruct the Cone from scratch, because the K-circle can be generated from the capping circle's center as a tangent to the Cone's sides.

But, the K-circle's center may be found by an even quicker method:
the upper intersection of the third row of the mapping circles marks the mid-point between the K-circle's center, and the tip of the Cone.

Measuring out 5 unit-circle radii along the Cone's sides is is the key to its solution, and simultaneously, a clear indication that the star to be imposed upon the Cone should have sides 5 units long.

        Abstraction of the Cone

     pentagram arms are divided into five units

Surprise # 3

The Cone creates the Square

Seeing the Cone described by unit circles equals seeing its geometric solution.
Moreover, if we review this solution with the Square included in the position, we realize that the self-explanatory Cone (of the Mother-star) dictates the Square. All we need is three of its circles: the K-circle, and two Unit-circles.

Procedure:

The Square's horizontal diagonal rests upon two of the unit circles.

The Square's center is at the intersection of the K-circle with the horizontal diagonal.
The Square's vertical diagonal rises from this center.
The Square's top corner is at the upper intersection of the K-circle with the vertical diagonal _ enough data to finish the job

I had the first substantial confirmation of my initial hypothesis _ the Stone Age engraving would prove to be scientific, somehow, in order to confirm the strong artistic impression of showing advanced technology.

Perception issues in manual drafting

Using straight-edge and compasses to draw the Cone & Square configuration had left me somewhat perplexed as to what exactly I was seeing in the result.
Does the Square duplicate the Mother-star's circumcircle on the Torso?_ In the diagram above, the outer circle of the Mother-star was copied to be concentric with the lower Square's circle. By the looks of it, the two differ by only a hair; and one isn't sure whether this discrepancy is due to accumulation of slight imprecisions in drafting or not. There were other things I couldn't be sure about; for instance, the star's outer circle looked like a perfect tangent to the upper right side of the Square.

Moreover, the middle-circle of the Cone, the unit-circle, and the inner-circle of the star circumscribing itsinside pentagon all seemed identical in size. But, were they identical? _ My curiosity went unsatisfied until I could check out the position in CAD _ on a $2,000, 10 MHz PC.

The Circle Triplets

In the diagram above, the three CAD produced circles - the middle-circle of the Cone, the unit-circle, and the inner-circle of the star circumscribing itsinside pentagon were made concentric, and then highly magnified. Yet, despite their magnification, these three circles still look much like a single circle. But, the following is true:

If the Unit circle's radius = [1]

the Inner circle's radius = [1.0040..]

the Middle-circle's radius = [0.9975..]

One mathematical consequence of this unit system: The side of a pentagon inscribed into the 'inner'-circle invokes the fraction of φ, the Phi-ratio.

        1.180339887... =    ((√5/2) - 1) x 10 or (φ - 1.5) x 10

        (1.180339887... / 10 ) + 1.5 =  φ

or (√5 + 1) / 2 =  φ    as well as (√5 / 2) + 0.5 =  φ

Now, measuring of the Cone by the unit-circles, making one side of the star 5 units long, begins to make sense.

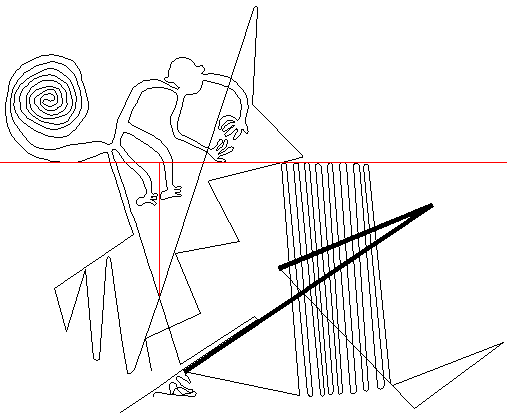
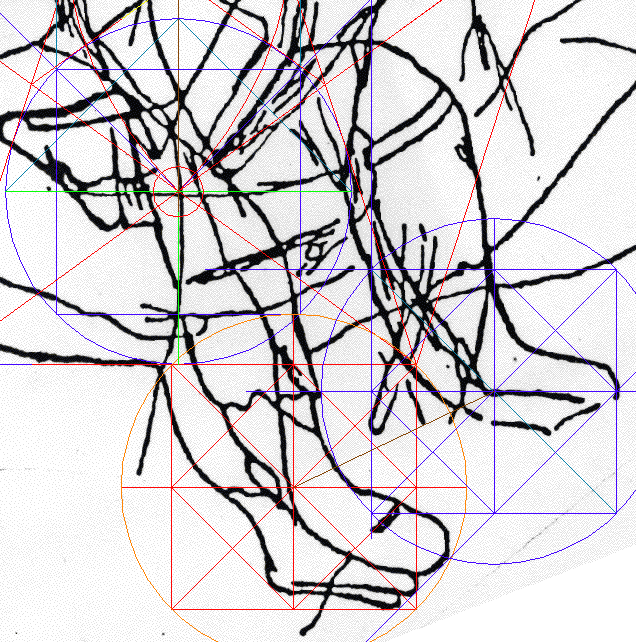
The Cone comprizes the cross-section of the Great Pyramid

This observation contributes to a series showcasing direct connections among the Giza pyramids, the engraving, and the monkey glyph.

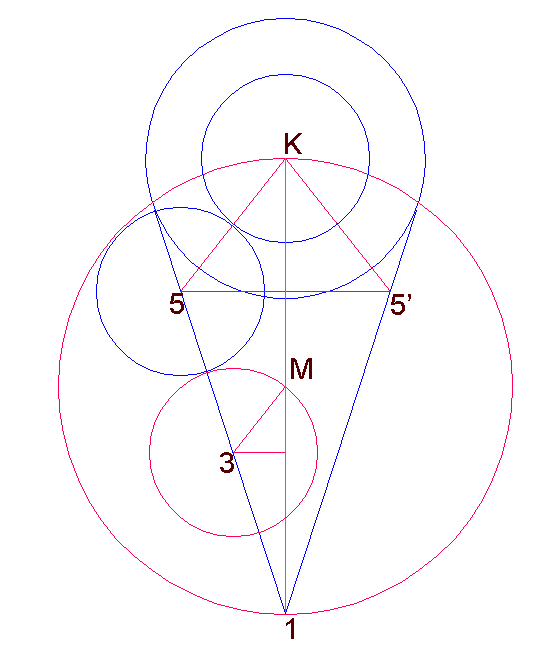
magic cone - the Great Pyramid crosssection

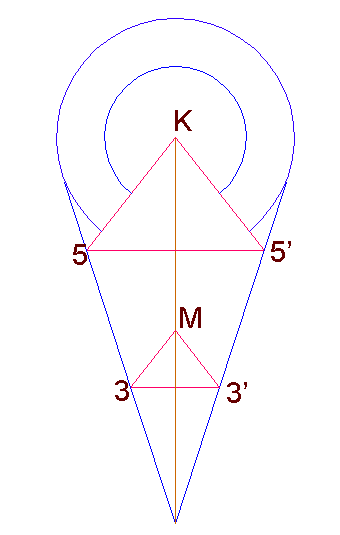
the Cone shows the Great Pyramid's cross-section twice

The two red triangles in the diagram are truly special:

1) Half the base of the smaller triangle has the exact value of minor Phi-ratio (φ - 1) or 0.6180339887...

2) The ratio of each triangle side with half the base is the exact φ - the Phi ratio.

3) The angle held by each side with the base is 51.82729237°, which rounds out to 51°50'.

A quote from Petrie:"On the whole, we probably cannot do better than take 51°50' ± 2' as the nearest approximation to the mean angle of the Pyramid.."

Our result of 51°50' complies to the ± limit set by Petrie.

Therefore, the Cone as described by unit circles presents the cross-section of the Great Pyramid and does it twice for good measure.

the π curiosity

If we double the base of the top triangle to eight-times φ - 1, the triangle height will be 3.14(460).
This direct statement of a close Pi approximation on a model of the Great Pyramid's cross-section is certainly noteworthy, because Pi is frequently discussed in studies and polemics regarding this pyramid.

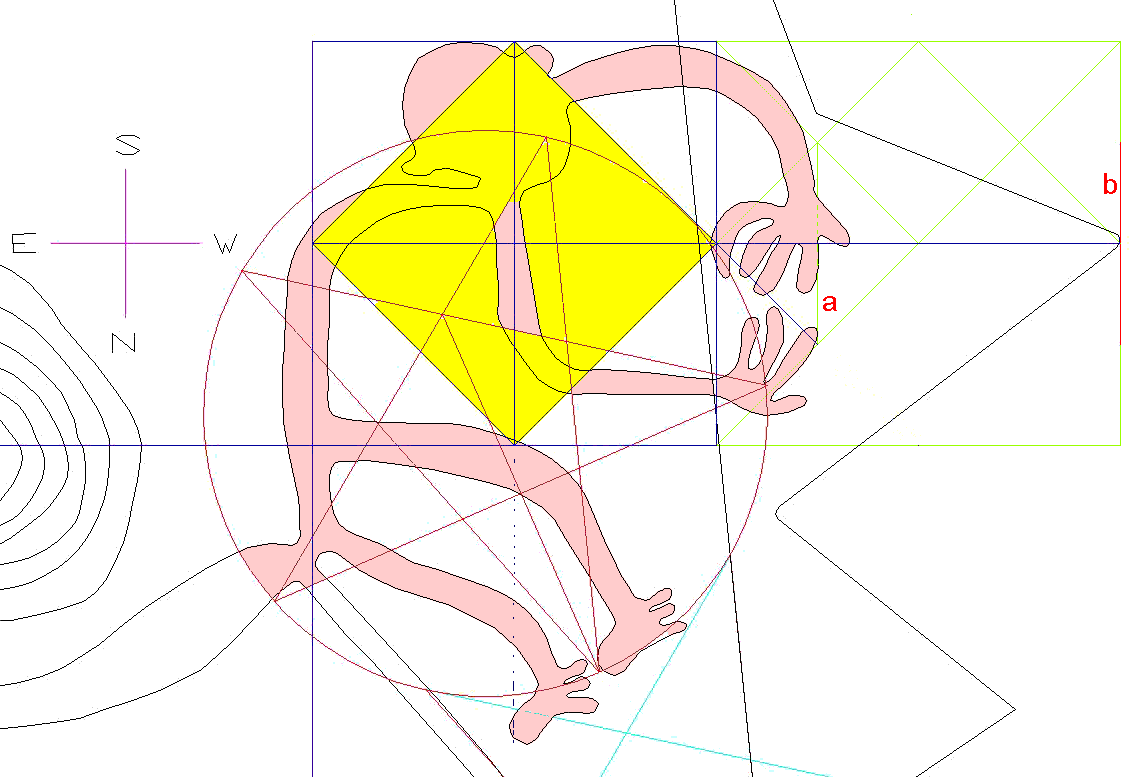
A telling line arrangement at the Square's bottom corner

Two of the Square's corners hold angles set by the Mother-star and only one complies to the Square

Extending from the Mother-star's center downwards through and past the bottom corner of the Square, the engraved line runs perfectly parallel to the left side of the Cone. Other lines in the area also duplicate the Mother-star's angles. All the lines together then create the 5-pointed star pattern we see in the diagram above.
Although more research is needed to determine this pattern's function in the overall clockwork, it definitely serves here as reassurance that the Mother-star's existence is no pipe-dream.

Getting Over Early Issues

Readers will recall that the Cone & Square position as given by the engraving suffers from one obvious, though mild, inaccuracy. Namely, the K-circle is not exactly as it should be in relation to the Square's center and upper corner. Its latitude above the x-axis is correct but its longitude is off a little to the west.

My hypothesis that the engraving and the advanced craft pictured therein (the Abydos Helicopter Effect) were the work of the same agency was therefore under doubt. There are no inaccuracies on currency bills printed by nations sending craft into space. By the same token, if the engraving were like a counterfait bill, an imperfect copy of the real thing, then its potential value, and of all the other engravings from the site, would be seriously damaged.

Accurate Inaccuracies

The inaccuracy of the Cone is accurately reflected by the Hip-lens as the centers of the Cone's K-circle, the Square and the Hip-lens remain on a straight line. This may suggest that the perceived inaccuracy may simply be a manifestion of motion, in which the K-circle with the Hip-lens pivot around the Square's center .
As well, some other parts of the design were apparently created from the Square and remained accurate with respect to it. Consequently, I formed an optimistic hypothesis that since the Square took over from the Cone in geometrical creation, it allowed the Cone itself undergo changes, because the original Cone (Mother-star) could always be recreated from the perfectly precise Square.

The Frame factor

Having the image blown up at nearby printers to twice lifesize made its exploration limited to manual tools much easier. The step had an unexpected consequence - it brought its units of length to parity with the metric system. Onwards, anything I measured by my metric ruler in millimeters yielded values intended by the designers.

About the simplest way of checking our image for signs of planning must be a look at its outer limits, as its main peripheral points are easy to see. These thirteen points are then connected by lines and the distances between them are measured and rounded to the nearest millimeter. The result is the 'Frame'.

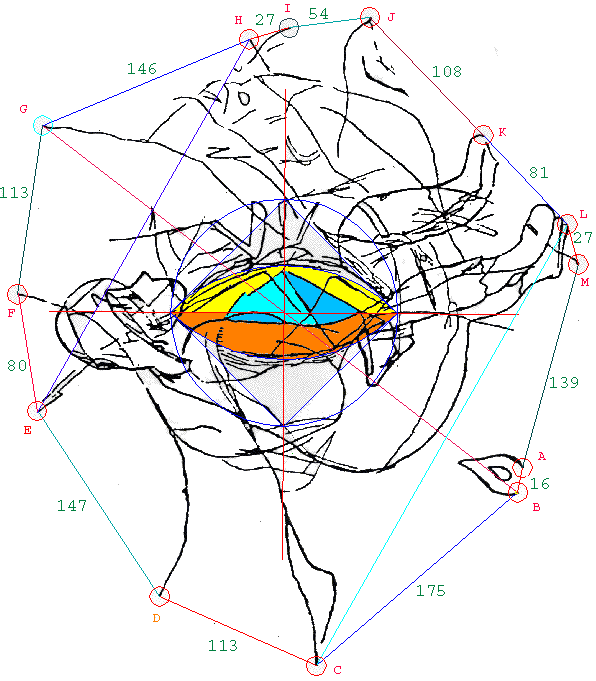
At the first glance, the thirteen whole numbers ranging from 16 to 175 are no big deal. But then one starts learning that these numbers, and their special arrangement, are simply ideal for the purpose of quoting Pi, Phi, and rates of Equinoctial Precession over and over, and as far as twenty-eight decimalse for Pi, ten decimals for Phi, plus, quoting rates for the equinoctial precession matching today's state-of-art.

The Frame looms as a stand-alone proof in the engraving's large portfolio of evidence proving advanced scientific level of its creators.

I firmly believe that no other set of thirteen whole numbers in a comparable range can rival the Frame at this type of communication. Promptly, I had issued a challenge to would-be skeptics to match the Frame with a similar creation of their own. And what do you know, by now, the gauntlet remains untouched in the middle of the arena for over thirty years..

To be fair, I even allowed the competition the use of a computer, as is evident from the below excerpts from the challenge:

Using a supercomputer, create and run a program following the below stated rules, with the same goal in mind.

Text omitted

My prediction is that in the end it will duplicate the "Frame" - the set of values from our engraving.

Text omitted

If the Frame's functions cannot be improved by rearranging and replacing some, or even all of its thirteen numbers, then the Frame must be the best solution in its category among the septillions, or so, of competing combinations possible.

When facing the reality of not being able to outdo the alleged blind chance, "skeptics" hide their heads in sandheaps, their last line of defence. Yes, I wax sarcastic, but such reaction is fully justifiable as a deserving and realistic portrayal of the deaf and dumb opposition.

Setting the System Correctly

There was a problem; the Frame units should be directly proportional to the unit circles forming the Cone. Instead, the unit circle's diameter came to 81 millimeters (with the image scaled 2 : 1).
Yet, in view of the slight discrepancy between the actual and the ideal models, was it possible that if the Mother Star were adjusted to the existing Square, the two unit systems would become directly proportional? The scanned image of the engraving was then imported into a CAD drawing and the hypothesis verified - the unit circle's diameter worked out to 80 millimeters even.
On a side note, there was remarkable synchronicity between my research needs and progress in the availibility of computer resources to the public.

How to Derive the Square from the Image

In order to let others reproduce and check my results, it's important to describe the process by which the Square is derived from the image, but first, allow me to make some cautionary remarks.
I cannot overemphasise how desirable it would be to work with the original instead of a mere copy. Consequently, there is bound to be some uncertainty. However, this uncertainty can be mitigated by results which closely and consistently conform with distinct abstract ideas of an exact nature inherent in the image, and that is what happens in this case. Stéphane Lwoff's claim that he and his team went to great length to accurately copy the image from the stone tablet is clearly true. The frequent occurence of near-microscopic accuracy of exact ideas evident at substantial magnification of the (copied) image is truly stunning. Considering that there must be some deterioration due to copying, the original can only be better. What is the limit? A molecular version of 3-D printing?

Orienting the Square

(It may seem strange that the x-diagonal is vertical here, but do recall that the first diagonal of the Square produced by the Mother Star was the x-diagonal; and the first diagonal (axis) is usually named 'x'.)
As seen above and below, both the x and y diagonals are supported in a number of places in the image. However, results will differ somewhat depending on our choice of supporting points, although this is only visible upon magnification. After many trial-and-error attempts, I settled on the following method:

1) The entire system is oriented by the y-diagonal, which is established rather easily, and in a manner guaranteed to produce practically the same result time and again:

The y-diagonal is propped against two distinct curves found on the engraved crosses approximating the western and eastern corners of the Square.

a) At the western corner of the Square located near Athena's back, the below cyan y-diagonal leans against the southern edge of an engraved curve. At this magnification the edges become somewhat hazy; so this is bound to create an error, but one so small as to be virtually insignificant.
Once we have the Square's center, its size will be set by a circle drawn from the center so that it leans on the western edge of the engraved cross - the red circle line pointed to by an arrow in the image below.

b) At the eastern corner of the Square located near Athena's bossom, the cyan diagonal leans against the northern edge of the curve in the engraved cross.

Numerous examples encountered in the study show that this diagonal must be so close to the original plan as to render the difference invisible to an unaided eye. Consider that if you have a 24 inch screen, you are looking at approximately a 200:1 magnification here.

In the diagram below, the western corner of the Square is visibly closer to the center, i,e, making the Square itself somewhat smaller (by a fraction of a millimeter). This is because the selection of the x-diagonal was done differently.

Setting the x-diagonal

After the y-diagonal is set, the angle of the x-diagonal is given automatically. Finding its actual position is not as easy. My selection from several similar possibilities was done by the trial-and-error method. (Hypothetically, these other possibilities could function as alternate settings for the Square - in case, the Squre itself changes, pulsates?)

For the best result, in my opinion, one should use the pair of points circled in yellow in the below diagram.

From the looks of it, these two points (line ends) are tasked with confining the x-diagonal between them. The magnified versions, seen below, show this very well.

The cyan-colored line is the x-diagonal, and it leans on the edges of the grey areas by each point.
The solid black of each point is very much the same distance from the x-diagonal; so the x-diagonal is in the middle of the channel.

Channeling as a method: Forming a narrow channel whose central axis proves to be the answer to a given problem seams to be a bona fide method. We can see this method used over and over in the geometry of the Giza ground plan.
It works as follows: we get two solutions, two lines which are very close to a line given by W.F.M. Petrie, Giza's most accomplished surveyor. The alternate solutions form a narrow channel whose central axis then duplicates the line given by Petrie.

Petrie gives states his measurements to the nearest tenth of inch (2.54 millimeter), so if our solution is within 1.27 millimeter of Petrie's - it is exact in the same terms.

................................................................ ....... ................

With both the diagonals in place, we draw a circle from their center so it leans against the outside of the engraved western corner of the Square (marked by the red arrow in one of the diagrams above).
The south corner of the Square then lands on the edge of the engraved line, as seen in the digrams below.

the Mother-star of Athena-engraving

The Square and the Mother Star form a set; therefore, given one element, the other one can be added correspondingly. In this case, we're adding the Mother Star to the Square, and deleting the Square for clearer view. There it is, the original star in the graphic below. Everything in the engraving can be traced back to this 5-pointed star.

Along with the star, the graphic also shows three small yellow squares and a rectangle extending horizontally through the upper half of the star - these are byproducts of the construction process which were assigned an important role.

The φ-square

Let's call the small yellow square 'φ-square', because it invokes the φ-ratio (Phi). Its base equals the length of the central section of a 5-pointed star's side.

When the whole side is 5 units long, its central section equals

1.180339887.. , or (φ - 1.5) x 10

The Golden Column

The first step in the star's construction (by the specific 13-step method) was the line numbered 1 (diagram above) which then became the star's vertical arm.
The circle, numbered 2, was the second step. Here, its diameter sets the thickness of the Golden Column (the horizontal rectangle) to its right. The column is divided lengthwise by the star into two upright golden rectangles with a square between them. Each combination of that square with the rectangle next to it forms a horizontal golden rectangle.

The Golden Column and the little φ-square are crucial to understanding the geometry of Athena's head, yet I had missed this line of analysis until I became aware of their role in the ground plan of Giza.
The plan's creation begins with the same 13-step construction of the 5-pointed star, so it was a clear directive to go back to the engraving and check for the Golden Column being unambiguously in evidence there.

The 13-step star construction method offers at least four ways of projecting the φ-square to the top right corner of the Golden Column. One of those seems to be given special attention.

The below shown position is based on the 13-step method. The two Q-circles are unique to this method. Drawing either one suffices to complete the star, but drawing both of these circles automatically recreates the φ-square at the top left corner of the Golden Column.

By intersecting extended sides of the green square these Q2-circles recreate the four corners (1,2,3,4) of the original φ-square at this location. From there it can be projected to the other top corner of the Golden Column.

Lines 'a', 'b', and 'd' in the diagram below give three more ways of projecting the φ-square to the top right corner of the Golden Column by golden diagonals emanating from key points on the original star.

Below: with the Athena-engraving as the background, however, the projection pauses at the moment when one of the diagonals of the moving square enters the tip of the Mother Star, because of sudden harmony seen between the head and the little square.

Harmony

An instance of perfect symmetry - cap Athena's head with a 45° pyramid - and its vertical axis will fit right over the vertical axis of the φ-square. This appears completely accurate until about 6 : 1 magnification.

The circle 3 shows that when the Golden Column is extended upwards by ½ of its height, its top side becomes an accurate marker for the top of Athena's head. It leads to the observation that half the Golden Column will form a well fitting frame for Athena's helmet (more on that later).

Mother Star's Tip Casts Rays

Below: With our attention focussed on this position, other surprises emerge into view. The two antennae rising from Athena's helmet (a and x) are rays cast from the Mother Star's tip at the center of the red circle.

Star angles

All the lines drawn in the diagram, except 'x', hold exact Mother Star angles.

That is a simple but far-reaching fact. Lines 'a' and 'g' hold 72 and 54 degree angles respectively with the horizon.
The line 'g' justifies its existence by being a microscopically accurate limit to two engraved lines pointed to by red arrows.
If we also discover where to position lines 'b', 'd', and 'e' we'll be able to accurately redraw the main outlines of the upper part of the head.
The line 'h' is another microscopically accurate limit to three engraved lines at once - also pointed to by arrows.
Lines 'i', 'j', and 'k' lean on engraved points on the left, while on the right they lean on the bridge of the nose, the bottom of the nose, and the bottom of the chin.

major straight lines of Athena's head hold Mother Star's angles

Five Parallels

Starting from below the chin and up to the line-1, we se five parallel lines. The bottom three originate from major points on the Mother Star; therefore, the face from the chin - to the nose - to the bridge of the nose is stratified in accordance with the star. The next parallel up originates from the (encircled) center of the Golden Column. The last parallel up originates from as yet unknown source.

Stars

All the star-angled lines can set up a number of stars. For example, in the below diagram lines 'b', 'c', 'e' and 's' create the star in view. The line 's' is a horizontal line drawn from the intersection of 'b' and 'c'.

The engraving is impressively well fitted to this star. It is more or less unthinkable that the artist/scientist would be unaware of it.

(apologies for the different lettering of lines)

A Snapshot

When the Golden Column is divided by axes into four equal rectangles, the two on the right are like a camera snapshot of Athena's face.

A Portrait

Adding an identical rectangle at the top produces a perfect fit with the top of Athena's hat (or helmet). The whole now looks like a classic portrait.

The Hatbox

The top two rectangles of Athena's portrait can be shifted directly west to become a nearly perfect containing rectangle for Athena's hat/helmet - the Hatbox. All of the white space inside Athena's helmet is inside the hatbox.

Exact Coordinates

Let's say that I want to draw Athena's face from memory using a computer . I know many exact coordinates for it in the context of the Mother Star and its products. I might begin from the 'Hatbox' - the right-side half of the Golden Column, which can be moved up by one-half its height and then shifted horizontally to the left to enclose Athena's helmet just like in the diagram above. But how far left?

The φ-square has its inscribed pentagram. Move the Hatbox left until the 45º diagonal drawn from its top right corner reaches the center of the inscribed star's horizontal arm. That shifts the original sides marked '1' into the position of the cyan lines marked '2'.

The cyan line '2' on the right tells me exactly how far the face extends in that direction.

Next, reduce the rectangle to a square whose right side is the cyan line marked '3'.

This line is then an exact boundary marker for engraved lines in three places, each place marked by a yellow arrow, the tip of the nose being one of those. The exact width of Athena's face is now known (left side of the φ-square to the line '3').

Thus, step by step, we gather information on the position of individual elements of the engraving. For instance, the star tip on the upper right side is at the edge of the engraved line. Drawing a 72º line through this tip will duplicate the line edge.

There is more relevant information to be gleaned from this diagram like the horizontal yellow line running along a line edge at the top of Athena's forehead. We see where it originates on the star; we can duplicate it.

The reader will find an in-depth analysis of Athena's head from the viewpoint of Mother Star angles in The Layout of Giza's Pyramids is at least 15,000 years old
The analysis actually extends to the entire image and confirms the importance these angles bear in the image.

A Suspiciously Fine Carving Technique

The inside and outside lines of Athena's nose are unlike each other. While the inside edge progresses practically in a smooth straight line, the outside edge is somewhat rough.
At the tip of the nose there is just one sharp turn in the inside line, compared to three turns in the outside one. Just below the tip of the nose the outside line edge turns towards the mouth in two long concavities while on the other side of the line the edge continues in an admirably straight line.
Next, on the inside, the line of the nose base turns smoothly to descend towards the mouth while there is a bump in the same turn in the outside.

Since lines in this engraving are on average less than 1 millimeter wide, it is hard to imagine how a single motion by the carver's hand would result in these effects.

Indeed, it does look like the two edges were engraved separately and not by hand.

Square's Domination of the Head Structure

One reason why I missed the relationship between the Mother Star and Athena's head for so long was being already aware of the major influence cast over it by the Square. The diagram below is an excellent example of that.
The green circle with an inscribed stare has its center in the north corner of the Square - lines 'a', 'b' are sides of the Square. The circle itself is the Square's φ-circle, which I usually refer to as the golden circle.

The star clearly sets comprehensive boundaries for the head's features.

Examples:

The star tip on the right - it connects to the top tip by a pentagon line, and to the far low tip by a pentagram line - these seem meant to set exact limits for the width of the face seen from that angle.

The upper tip - its coincidence with the engraved features is simply spectacular. It is also planted in the most important point of the system. For confirmation, one only has to observe how regularly one sees this point, or its immediate area, involved with the designs throughout this account. Interestingly, this location is at the front center of Athena's frontal lobes. <health.qld.gov.au/abios/asp/bfrontal> quote: The frontal lobes are important for voluntary movement, expressive language and for managing higher level executive functions. Executive functions refer to a collection of cognitive skills including the capacity to plan, organise, initiate, self-monitor and control one’s responses in order to achieve a goal. The frontal lobes are considered our behaviour and emotional control centre and home to our personality.> This is truly a telling selection because Athena's frontal lobes are thoroughly connected to all geometric elements of the system indicating her awareness and control over all of it.

There is also an exact limit for the lowest point of the helmet.

There is also an exact limit for the lowest point of Athena's chin.

There is more order to be observed if one roams over the picture.

Square's corner at Athena's head, also center of the star

Supreme Accuracy

The circle shown below is centered in the star's tip, exactly positioned on the edge of a line, is an accurate limit to the three white areas pointed to by arrows. Considering the approximately 20 : 1 magnification of the scene, this is truly impressive.

Convergence of Influences

The outer line edges radiating from Athena's forehead conform with the Mother Star angles, rather than those of the Square.
Already at this stage, the Mother Star and the Square combine to a create an ever more detailed map of Athena's head,

Reappearance of Athena's Cone & Square Module in the Nazca Monkey

The Cone & Square module is a sophisticated geometric engine. It powers the Athena Engraving. Its very existence, other than in my imagination, was never taken seriously. I was lucky and found some interesting coincidences - happens all the time.

In 1992, after showing my findings to some people in Prague, I was given a small picture of the giant geoglyph of a monkey from Nazca, Peru by Mrs. Z, Hrubá. She wondered what geometry might be there to discover...

Did her subconsciousness see in the monkey what I was describing in Athena? The monkey stands inside a large X- shape (the X-Tree) whose angle begs checking out by resembling a 5-pointed star. Moreover, the monkey's arms mimic a square.

an blatant balance of the Nazca monkey glyph

an blatant balance of the Nazca monkey glyph

The long arms of the X-Tree are blotted out in the image below - by sides of 5-pointed stars. If there were to be the Mother-star here, it should be the one centered on the monkey.

The Cone part of the Mother-star runs parallel with the X-Tree sides. It is shown in magenta in the below image.

the purple Monkey-star is the one which the square isderived from

Below: The Square part of the Cone & Square module is shown in yellow. Its lines are a perfect fit to the monkey. (see this chapter for details)

Unlike in Athena, the same square cannot be accurately distilled from the image; it has to be positioned there by the Mother-star. However, the Square's diagonals seem to coincide with the world compass really well.

Below: The containing rectangle for the monkey formed by lines in the directions of the Square's diagonals. The image comes with a manifest proof that this rectangle is a containing rectangle for the Golden Triangle. Also in sight below is a containing square for the monkey's feet.

The top right corner of the containing square on the feet connects to the top and bottom corners of the Square closely imitating sections of a 5-pointed star.

this position shows an incomplete 5-pointed star which begs completion

this position shows an incomplete 5-pointed star which begs completion

Extend B - C from the image above up to the horizontal diagonal of the Square.
Next, mirror the A - B and extended B - C across the vertical diagonal of the Square. The result is the diagram below - an excellent facsimile of the regular 5-pointed star.

extended lines give an excellent facsimile of a 5-pointed star

How excellent a facsimile it is can be seen upon merging it with a true exact star. The result is below.

an Eye Opener

In the lower corner of the Square, the Square's golden circle with an inscribed square forms an orderly harmonious position with the circled containing square for the feet (the Foot-square). This brings one thing to our attention - the golden circle and its inscribed square are meant to be exactly the same as the Foot-square with its circle.

Nazca monkey's clues here create an excellent facsimile of the regular 5-pointed star

When concentric, both circles and their inscribed squares look like the diagram below. Although there are two separate circles/squares here, we only see one.

Below: The design by itself. The containing square of the feet is the same as the square inscribed into the Square's golden circle. This position implies a specific 5-pointed star construction, also shown below. Altogether, it takes 13 steps.

Construction of the 5-pointed star in 13 steps

first six steps to a construction of the regular pentagram by the compases & straightedge method

The diagram above shows the first six steps. Step-1 is a horizontal line, and already an arm of the sought after star.

Construction of the 36-degree angle

construction of a regular pentagram in 13 steps

construction of a regular pentagram in 13 steps

step 7: Draw a line between points C and 2.

step 8: Draw a circle centered in 'C' through the intersection of the blue circle-2 with the new line.

steps 9&10: Draw lines from the top of circle-3 through points P1 and P2, which are the intersections of circle 'C' (yellow) with circle-3 (green). These lines are tangents to circle 'C', and the angle betwen them is exactly 36 degrees. They represent two more sides of the star.

Construction of the regular 5-pointed star _ steps 11,12,13:

The points 1 and 2 are there from the previous diagram. Now it can be seen that a circle from the point C, through 1 and 2, shall be equidistant to the points 3 and 4.
For the final two steps, draw lines from 3 and 4 through C to meet the horizontal line from step 1, and the pentagram is complete.

alternatives for steps 11,12,13:

Since the horizontal line will serve as one arm of the star, the point 'Q' circled in green will be equidistant to points numbered 1, 2, 3, needed to complete the star (Q could be on the other side as well).
point Q gives four points of the star - two tips - two corners of the inside pentagon

point Q gives four points of the star - two tips - two corners of the inside pentagon

The Trans-Atlantic Connection & the Foot-square

The Foot-square (containing square for the feet) theme seems to be the culmination of monkey's geometry. Not forgetting that success of my analysis was due to the hypothesis that the monkey's geometry duplicated the Athena-engraving's basic geometric system, I had to wonder if Athena's system included the Foot-square idea as well. It turned out that Athena gives this idea quite an in-depth treatment.

The Athena-engraving already has its Square; so we just add the 13-step star with the Foot-square to the template. We have to rotate it 90 degrees; however, so it points towards Athena's feet (diagram below).

By the way, unlike the barefoot Nazca-monkey, it's clear that Athena has footwear on. To me, it looks like a heeled boot with a stirrup on her left foot, and something not so easily identifiable on her right. Whatever it may be, it is startling in that it has three toes just like the monkey.

feeding back the position from Nazca to La Marche shows mighty correlation

feeding back the position from Nazca to La Marche shows mighty correlation

The circle around the Foot-square (the Square's Golden-circle) clearly centers upon Athena's right leg below the knee. Whereas at Nazca the Foot-square covers both feet, here it covers just one, because the designers had availed themselves of the greater complexity of Athena and expanded the Nazcan idea into a system of two Foot-squares.

same foot-squares fit both feet

The Foot-square, along with the smaller squares inscribed within, is clearly custom-fitted to the lower leg and the foot; with the exception of its left side, all the other lines define the foot in some way. For instance:

* the bottom line of the square does exactly the same thing here as in the monkey glyph - it limits the right foot from below and does it with extreme accuracy;
* its right side is a perfect limit for the middle toe;
* one side of the smaller inscribed square forms such a limit for the heel.

The other sides of this smaller square, the diagonals, and the axes all relate to the engraving in a meaningful manner. I skipped listing the numerous instances of it for the sake of brevity.

the other Foot-square

I also tried moving the Foot-square over Athena's other foot just by eye, to see how it fits there. The move was sound:

* the width of the left boot including the stirrup, is the width of the Foot-square;
* counting from the top of the left leg, the line of the left side of this square relates meaningfully to the engraved lines in the area fully six times;
* the horizontal axis also correlates with the engraving strongly;
* the extended right lower side of the inscribed square is a perfect boundary to the three toes of Athena's right boot. As a rule, neither monkeys nor humans, not to mention boots, are three-toed; so this 'coincidence' cements the special relationship between these figures.

an unexpected "coincidence"

For good measure, moving the Foot-square over Athena's head results in an amazingly precise fit. It is shown below at about 2 X lifesize (inscribed in the Square's golden circle along with a star).

the same square expanded into a golden rectangle

the head area as a whole is a very good fit to the rectangular form based on the Golden Section - two squares side by side sitting on top of two upright golden rectangles

The head area as a whole is a very good fit to the rectangular form based on the Golden Section:
two side by side squares sitting on top of two upright golden rectangles.

The bottom line of the golden rectangle nestles neatly atop an engraved area (arrow).
Its left bottom corner is likewise at the edge of an engraved line.
The top of the head to the face 1 / Φ = 0.618..
is as the face is to the entire head Φ / (Φ+1) = 0.618..

Overall, the height of the head is Phi + 1 ( 2.618..), and its width is 1 + 1.
The vertical distance from the bottom of the chin to the top of the head is about 4.5 centimeters. It probably is a lot more than that on your screen, I hope, for the sake of having a good view of the accuracies.

So, overall, the experiment of testing the concept learned from Nazca to the Athena-engraving worked out beyond expectation. I had found three prominent instances of the Foot-square in Athena. Along with the previously discovered material, it was enough confirmation for the initial hypothesis. Satisfied, I went on to other things.

Following the script

Years later, and after much progress on other fronts, I returned to these Foot-square phenomena in Athena. I got the initial Foot-square by construction, but the other two by just shuffling it about the figure. Yet, I knew that there had to be a correct way to do it by exact design because that's how the Ancients did everything else.

The Foot-square is inscribed in the Square's golden-circle used in construction of a 5-pointed star; so it's natural to experiment by also inscribing the circle around the Foot-square with a star of its own.

The Monkey-tree

The experiment then presented a view of striking harmony between this star and the engraving. A detailed description here would be counter-productive; instead, I marked most, but not all, instances of it by arrows. Still, some of these correlations are simply in the must-mention category.
The passage of star lines a & c through the image is the most blatant correlation as these merge with the engraved lines over long distances, long enough to set the legs' basic directions.
Lines a & b and b & c create 36-degree cones.
Lines b & c actually give two 36-degree cones oriented tip to tip on the same axis.

This is a deja-vu of the Nazca-monkey's X-Tree!

Along with Athena's three-toed boot, this reoccurrence of the X-Tree (call it Athena's Monkey-tree) is overwhelming evidence that the two works come from the same source.

Here we see an analogy to Nazca-monkey's 36-degree X-tree, two cones tip to tip.

Here we see an analogy to Nazca-monkey's 36-degree X-tree, two cones tip to tip.

Line 'c' of the Monkey-tree is given by the pentagon inscribed into the golden circle. Accordingly, when assigning stars to the Monkey-tree, let's make their sides the same length as on this pentagon (see above).

Mirror these X-stars as in the above illustration. The new stars reveal the exact positioning of the second Foot-square. It begins with line 'e', which, by the way, the engraving also echoes; and which also passes through the immediate area of the Square's easternmost corner.

Above: The small half-green circle on the right marks a point where star lines associated with the Monkey-tree system intersect at the edge of an engraved line. It is the same as the midpoint of the right side of the second Foot-square which I first positioned there by eye. Now it is the true insertion point for the second Foot-square.
For confirmation, a line drawn down at 45-degrees from this point is an accurate boundary to the three toes of Athena's right boot, just like before.

Above - a detailed look at the two Foot Squares:

The direct connection between their centers is immediately interesting because out of two chances at becoming an accurate limit to engraved lines, it does just that. It limits the reach of the Monkey-tree downwards on the right side; and it limits the reach of white space between the heel and the sole of Athena's right boot. Of course, two out of two is yet another attestation to the direct connection between the two Foot-squares.
The first time, it was the circled Foot-square which based entirely on the golden-circle of which it is a duplicate. The same principle applies the second time as well. The other Foot-square is entirely a product of the first.

Athena's head & the Foot-square - the Halo-circle

Is that a halo around Athena's head? It's an exact duplicate of the Square's golden circle, and its location is given by a method much like the one we used to position the two squares on Athena's feet. Namely, each of those was derived entirely from the nearest golden circle.
Here, it is almost the same case. The nearest golden circle is centered in the nearest corner of the Square, and it does participate in the process.

Lines 'a' and 'b' combine to give the line 'c'.
Lines 'd' and 'e' combine to give the line 'f'.

Lines 'c' and 'f' belong to the star and the square inscribed in the Halo-circle and combine to give us the insertion point for the Halo-circle.

Below - the golden circle centered in the nearest corner of the Square:

Lines 'd' and 'e' are parts of the star and the square inscribed in this circle;
line 'a' is a starline originating from the center of this circle; see that it is parallel to 'f'.

The line 'b' is the only one to come from elsewhere - we see that it is the extension of a side of another square covering the upper part of Athena's head. This other square is absolutely key to understanding the head's architecture. The reader may be surprized to hear that it actually represents the base of the Great Pyramid.

This other line 'b' only became available after exact recreation of Petrie's ground plan of the three big pyramids of Giza from our familiar Cone & Square configuration. Testing the validity of such method called for its importation into Athena and its geometry, as well as the monkey, of course. This is the subject of other chapters.
Yet, there is another way to place the Halo-circle/square. It is shown below, and it involves a star whose height equals half the Square's diagonal. You can see that the middle of its base rests on the Square's corner. However, this recreation of the square within the Halo-circle is a tiny fraction of a millimeter lower than the square fitted to the head by hand, whereas the first method does recreate it with microscopic perfection.

From Head to Toe - the Square's Column

As we all know the credit for the column's idea goes to the Nazca Monkey. This column has some surprizing qualities.
The figure of Athena is engineered to fit a configuration based upon the Square

The figure of Athena is engineered to fit a configuration based upon the Square

The Square's 'y' diagonal sets the column's width. Its height is also derived from the Square:

Mirror the top half of the yellow Square upwards, and its top line will mark the highest reach of the (white) internal space in Athena's head - the top of the column.

The bottom line of the Foot-square sets the bottom of the Square's column.

There are two more columns to look at here - one created by the golden circles centered in the top and bottom corners of the Square, and one created by the squares inscribed in those circles. The engraving is visibly attuned to all the three columns.

A-B-D-E in the diagram marks a golden rectangle, one of several in view.

Virtually Exact Star-maker Template

The Square's Column has an amazing property: the angle of its diagonals with the horizontal is 24.0000356.. degrees, which is supremely precise.
The difference from perfection is a little less than 1/8th of a second of a degree, or approximately 1/10,000,000th of the circle. ( a second of a degree in decimals is 0.00027777.. , or 30.864 meters in planetary terms.

24 degrees comprise 86,400 seconds - just like a 24-hour period. If this were a mechanical watch, it would be off one second every eight days - the best ever.

(For comparison, the Swiss watchmaker Zenith has unveiled a watch in 2017 called the Defy Lab which it claims is the most accurate mechanical watch in the world. Its precision rate of just 0.3 seconds per day far exceeded the standards for COSC chronometer certification.)

(An interesting tidbit, in units set by the mother-star, the circle around the column has an area of 66.66.. )

The diagram becomes an illustration of the following rule valid for all inscribed rectangles:

Draw a line from a rectangle's corner to where the rectangle's long axis crosses the describing circle; it creates an angle with that axis which is exactly half the angle that axis holds with the rectangle's diagonal.

Moreover, our rectangle automatically produces the meaningful angles of 12; 24; 36; and 48 degrees. Hence it allows the division of its circle into 30 equal parts (diag. below).

This head-to-toe rectangle set by Athena's figure is a practical template for inscribing a number of regular pentagrams and hexagons into its circumcircle:

Connecting every sixth point on the circle creates a pentagon, every fifth point a hexagon. With thirty points on the circle, six 5-pointed and five 6-pointed stars will be in sight in the end.

Monkey's Impact

Without help from the Nazca Monkey, as long as there was just the engraving, I was being accused of inventing its Cone & Square spirit. Therefore, the Nazca Monkey coming to the rescue was like a miracle. Its intervention removes the burden of responsibility from my shoulders as it decides the issue of who is the creator of the Cone & Square system in favor of the prehistoric agency. Moreover, it guided me to some of the engraving's secrets, which I had been oblivious to up till then.

Any number of designs claiming descent from a particular five-pointed star can be brought to the same scale and unified for comparison with the others by that star.

Of course, this principle only applies if such stars exist in reality rather than in imagination.
The Athena Engraving and the Nazca Monkey glyph are vastly different from each other in size. In the image below, the two were scaled and positioned so that their respective 'mother' stars merged and became one and the same. Both works were thus presented on the mutually proper 1 : 1 scale.

Geometrical Modules in the Torso

Most of the lines in the torso create significant angles with the Square's diagonals x, y. These lines together with the Square's diagonals create rational order, a geometric module.

The straight lines 'c' and 'a' subtend irregularly curved engraved lines. Drawing subtending lines presents a way of finding a simple meaning for complex multi-purpose lines.

In contrast, the straight lines 'e', 'b', and 'd' stay within the engraved originals.

From left to right:
Line c holds a 30 degree angle with the x-axis.
Line e holds a 36 degree angle with the x-axis.
Line a holds a 36 degree angle with the y-axis
Line b holds a 36 degree angle with the y-axis.
Line d holds a 30 degree angle with the y-axis.
Line f holds a 36 degree angle with the x-axis

Lines a and b create a triangle with the Square's y-axis, which is found on a regular 5-pointed star (36x36x108 degrees).

I had used compasses to develop the triangle into a 5-pointed star, utilizing the blue circle from diag. 19 below. Right away, what was a simple though artificial idea, advances into the complex category.

The result is spectacular because one of the star's corners falls into the center of the Square, and the star's top two corners connect by a line which goes directly to the Square's corner 'D' on the right. It is clear that this star results from Golden Section operations on the Square.

Moreover, the star's axis which creates the F-point on the blue circle was joined there by the line 'd' from the second diagram up. This meant that by reversing the process, we can recreate the line 'd'.
Next, I learned that a line drawn from 'F' at thirty degrees to the y-axis intersects it at the same point as line 'c'. A line drawn from that point at sixty degrees to the y-axis recreates the original line 'c'.

Therefore, the entire position as seen in the diagram below is exact and can be reconstructed by geometric means.

The initial star, the Pyrostar can be expanded into a larger stage.

This pentagonal side of the Pyrostar coincides with the 36 degree angle constructed from 'D', and is a tangent to the so called Golden circle centered in the opposite corner of the same square (see below).

The Pyrostar, and the Square's minor Golden Rectangle

This Golden Rectangle (actually white in the diagram) has the length of the Square's diagonal, and the height of the Golden circle's diameter. It is safe to say that it fits the engraving beautifully, see the second diagram down.
Below, three Pyrostar lines - two of which are the outside pentagon sides - are tangents to Golden circles in diagonally opposiite corners of the Square.

The big circle in the diagram below divides the Square's horizontal diagonal in the Phi ratio, and sets radius of the Golden Circle, It is centered at the 3/4 point of the Square's horizontal diagonal, and passes through two corners of the square.

All the adjacent segments set by the series of points R-00-G-L-M form the Golden-ratio:

segment R-00 / seg. 00-G = seg. 00-G / seg. G-L = seg. G-L / seg. L-M = 1.6180339887.. = Phi

The torso's width is well contained within the band of the Golden Rectangle's width (the height of the Golden circle). This is clearly visible.

All neighboring segments set by the series of points R-00-G-L-M form the Golden-ratio

Nested Circles

This is a repetitious phenomenon - a circle, part of the inherent geometry, finds itself contained by the engraving. In the image below we see two concentric circles centered in the 3/4 point of the Square's horizontal diagonal. Both circles are golden; the large circle divides the left half of the diagonal by the Phi-ratio. The small one also involves the Phi-ratio; one can see exactly how by its relationship to the pentagram in the upper half of the Square, and to the Square's golden circle.

Above we can see a strong indication by the engravers of the Golden Section in process within the Square.
The big circle is one of the four such possible circles (one for each quadrant), and it definitely fits the engraving, in at least twelve places. Refer to it as the 12-point circle.
Concentrical with the 12-point circle, is the small brown circle in the diagram below. Its diameter forms the Golden ratio with the diameter of the Golden circle itself, as seen from the star in the diagram above. Like the 12-point circle, this small circle also fits the image neatly.

It is wedged between the lines a and b (which create the Pyrostar), and lines d and g. So far, the engraved line 'd' translates into a straight line passing entirely within the engraved line. But, one diagonal of a Golden Rectangle originating from the point D of the square, subtends the engraved line 'd' with good accuracy. An engraved line of the Torso is symmetrical with the line 'd' across the x-axis.
So, the enclosure of the small brown Golden circle is consistency itself. One Golden circle and four lines, each having to do with the Golden Section within the Square.

The Square's major Golden Rectangle

This is the Golden Rectangle, whose height equals the diagonal of the Square.

Global Connections

This chapter gives more examples on how one geometrical system unites two ancient designs, each from a different continent and age. An unidentified prehistoric agency has had global influence over our planet and created art and architecture as mathematical puzzles for future generations:

We look at:
a) the monkey figure from the world renowned Nazca Lines, Peru
b) a 14,000 years old engraving from the not so well-known grotto of La Marche, France

The elements common to Athena and the monkey tend to lurk at a different depth in each. When observing a given property in one work which escapes notice in the other, going back to check for its presence there often works out. The same is true about going back to these two works with the Giza layout - it was a revellation. Therefore, the three are best analyzed together.

A star brings us together

The monkey from Nazca spans a hundred meters, while the engraving from La Marche tangles its lines over a portable A-4 sized stone tablet. Each had gone through being a 5-pointed star in its embryonic stage; duly, the two can be scaled 1 : 1 by scaling the works until their mother-stars become the same size.The two works can be merged for comparison by fusing their mother-stars into one.

This idea is implemented in the image below. Out of the three Giza pyramids only the Great Pyramid si shown, in order not to clutter the view, The original star is divided into left and right halves by a central axis. Athena's head and the Great Pyramid are to the left of that axis; the monkey's head is to the right, and is away from the pyramid.

Merging of the Athena Engrasving with the glyph of Nazca Monkey on a 1 to 1 scale

There is some duality in view: The heads are at approximately the same elevation, and a tip of the star is inserted in each head.

Face Merging

These attributes are reflected across the stars vertical axis - so, why don't we mirror the entire monkey across this axis to see what happens?
The outcome is spectacular in that Athena's face is now almost one-hundred percent inside the monkey's face, and her right eye now doubles as the monkey's right eye!

The spiral tail looks quite well fitted to Athena's feet.

In the next experiment; without any rotation whatsoever, we move the monkey's head over the head of Athena to see how the two fit together.

A Perfect Fit

We could not have hoped for a better result! It looks like the Agency had built in confirmation of our scaling procedure.

the monkey rotated 54 degreed (an angle found on the 5-pointed star) around the original star's center. Again, there is an almost perfect containment of Athena's face inside of the nonkey's face.

Except for a tiny sliver, Athena's face is once more completely contained in the monkey's head.
Its hands, esppecially the left one, are clearly attuned to the engraved lines of Athena.
The space around the star's center can be seen as a dial divided into multiples of 9 degrees - angles
created by the pentagram. In that case, a rotation of 54 degrees is one of the expected possibilities.
As well, the right side of the X-tree - both its straight part and the triangles to the right relate to Athena's lines in a significant manner.

The Best Circle Expressing the Arc of the Monkey's Cranium

A parallel to a side of the Mother-star drawn from the Hand-circle's center draws attention because its passage through Athena looks non-random, as it passes through the corner of the pyramid pictured in the torso and rests on a couple of arcs. the last of which belongs to Athena's helmet.
Since this parallel looks to have some dignificance and cuts a golden triangle out of one tip of the star, I experimented by completing that triangle into a smaller star. One of its arms then merges with a line of the torso, and the engraved line next to its right passes right through the small star's center.

But the same line is already a side of another star, as seen in the image below, so this is interesting.
Moreover, the same line also passes right through the center of the monkey's head.
The same line serves as a line of centers for three circles:

a) the newly created star's circumcircle
b) the same size circle is the best fitting circle for the circular top of the monkey's head
c) a smaller circle expressing the arc of the cupola on top of the torso disc

The same circle, best expressing the arc of the monkey's head, is seen in greater detail below.

More fantastic than science-fiction, the high level geometric union between the Athena-engraving and Nazca-monkey is a fact of life. Yet, it would not be complete without the ground plan of the three great pyramids of Giza. The three are one - a trilogy. This trilogy could not exist without having a shared backgroundof advanced knowledge and technology.