

| Exact recreation of
Petrie's Giza ground plan from Golden Section ideas Introduction In 1883, Sir W.F. Petrie published his geodetic survey of the Giza pyramids. It stands unsurpassed till this day and is the standard reference for anybody interested in Giza. Theorists believing that the mutual positioning of the Giza pyramids is not random but due to a site plan have ever since made attempts to prove their belief by reverse-engineering Petrie's map. The plan is a monumental puzzle with abundance of potential design ideas. A number of plans has already been proposed; however, none of the reconstructions have gained general acceptance, mostly because they're not accurate enough, but also because there are great many competing theories - which is the right one? A plan by J.R. Legon gets some key things right; other plans suffer from major inaccuracies in mirroring the actual position of the pyramids. It then becomes difficult to prove that it was the one design idea which had governed their building. A deceptive factor While many elegant design ideas differ from the surveyed dimensions by a foot, or more, those still look absolutely accurate on even the large screens. For example, on a display of 35 x 35 inches, their inaccuracy is diminished thousandfold - a foot then becomes a thousandth of a foot which is invisible on even a high resolution screen or a drafting board, not to mention diagrams drawn in thick lines. The Giza design and Psychology Among other things, the Giza design is also a mirror for the human nature. Instead of pooling individual observations and theories into a coherent body, researchers embrace the principle of mutual exclusivity; therefore, their ideas are the only right ones. Yet, all these ideas collectively form layers of meaning around the core of exact construction. I suggest that the Giza designers were aware of all that and had chosen their plan because of this wide range of choices facing those in the generations to come, who would want to solve the puzzle and reconstruct the true plan. To enable the future solution of the puzzle, extraordinary accuracy in the plan's implementation was a must. Followed up by W. F. Petrie's accurate survey of the site, a solid basis became available for a credible reconstruction of the planning process. As for my own involvement with Giza, I was skeptical of having any chance to contribute to the existing body of research, the result of many years of effort by many scholars. The change of attitude came after I had made a successful foray into the controversial "Abydos Helicopter" scene from Seti's Abydos temple. Egyptologists persist in explaining it away as a so called 'palimpsest' _ an accidental fusion of unrelated glyphs. As such, its nature has to be chaotic. I had supplied a solid proof of the presence of a thoughtful geometric order in these glyphs,thus effectively debunking the official explanation. The Abydos Helicopter glyphs are not a palimpsest; it's as simple as that. And since the mainstream took no notice, its approach is now clearly partisan. Abydos Helicopter was the encouragement I needed to eventually contemplate the Giza ground plan. For starts, I copied the position of the three pyramids as surveyed by W.F.M. Petrie, and listed in an article by John Legon, into my CAD program. Initial Observations - The Pyramid Square & Khafre's Pyramid The first step I took was extending the enclosing rectangle (blue in the diagram) of the three pyramids, ubiquitous in other studies, into a square. Taking this simple step is absolutely vital to opening the floodgates. It is strange that hardly anyone had tried it before me despite well known facts which should encourage it. For instance, Corinna Rossi on page 122 of "Architecture and Mathematics in Ancient Egypt" says: "From the Middle Kingdom onwards, ancient Egyptian artists used square grids.." Well - why not earlier? After all, the pyramids themselves are square.   Golden Section The Pyramid Square is divided by the Golden Section lines (green) from each direction. Altogether twelve golden rectangles are in sight. In the center of the Pyramid Square is a small square extended by a golden rectangle on each side. This formation represents a golden-cross. The Second Pyramid's vertical axis is very close to the vertical axis of the Pyramid Square. Does the square of the Second Pyramid mimic the one in the center of the (green) golden-cross? A follow-up experiment A golden-cross is extrapolated from G2's (Khafre's) square and made concentric with the Pyramid Square. Now there are two Golden-crosses superimposed over each other for comparison. The similarity in size is striking.  At this resolution, the two superimposed crosses create an illusion of there being only one cross. The actual ratio of a side of G2 to its distance from the Pyramid-square side is 1.61 _ the first three digits of Φ after rounding the actual result of 13,619.1 : 8,474.9 = 1.60699.. Is it a mild hint that the design of Giza has something to do with the Golden Section? In the diagram below, golden proportions, added to the G2 in situ, seem to find some correlation to the south side of G1. Here as well, we encounter somewhat rough facsimiles of golden rectangles. 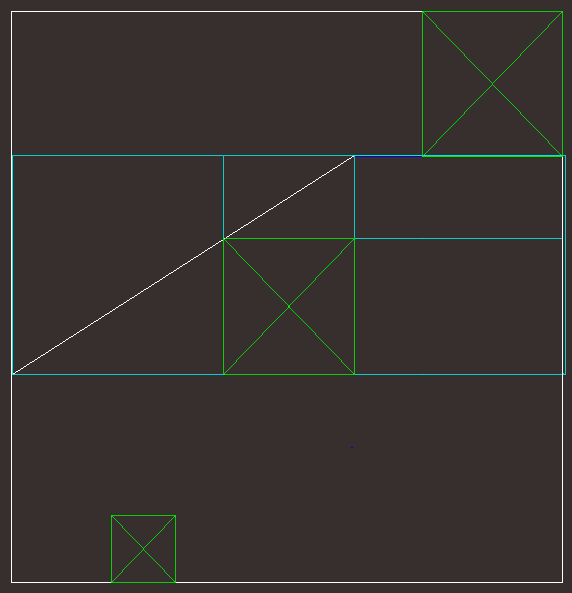
The results were thought-provoking, so far. In this new framework, some prior interesting, but seemingly dead-end, observations by others suddenly become meaningful. Not wanting to rediscover the wheel, a search was in order on the subject of Giza layout. Soon, I had found an informative article over at Jim Alison's site: http://home.hiwaay.net/~jalison/gpsp.html It deals with work by John A.R. Legon, Chris Tedder, Robin Cook, and Jim Alison himself on various notions of a Giza ground plan. * Chris Tedder had noted that perpendicular distances between the pyramid centers produce two golden rectangle facsimiles (ABCD, and DEFP) and proceeded to propose a plan that the Egyptians had possibly used. Unfortunately, these rectangles have poor accuracy. 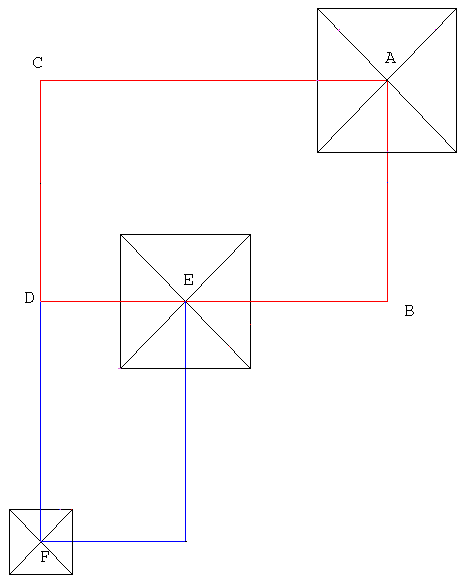 The ratio of BD to BA is 1.623 instead of the desired Golden Ratio of 1.618.. The BD segment is 74.28 inches too long for a correct golden rectangle. The ratio of DF to DE is 1.605, which is more than twice as bad. Judging by these facts, the level of builders' skills, or knowledge is not impressive. But I learned that reality is different; the builders are scapegoats for our incomplete analysis! Space-age Accuracy in Implementation of an Exact Idea It may sound bombastic, yet the heading above is realistic. It is a taste of what's to come in this reconstruction. To see how out-of-this-world good the builders were, let's approach the same position a little differently:  1) Draw horizontal and vertical lines (axes) from the pyramid centers. 2) Draw an exact golden diagonal from the intersection of 'd' and 'e'. (Any rectangle with this diagonal is a true golden rectangle.) 3) Draw lines 'h' and 'g' from the intersection of 'c' and 'f'. Now, the rectangle formed by lines a-b-c-h is an extraordinarily accurate golden rectangle: Instead of 74 inches, the "inaccuracy" of its long side now stands at 0.18 inches over the distance of 17,833.8 inches .. The ratio of sides in this golden rectangle is 1.618021, which is just 0.00001 off the true value of Phi. The line 'g' is an extraordinarily accurate golden diagonal: Instead of the correct 31.71747.. degrees, its angle is 31.71767.. mere 2/10,000 (half a second) degree off. Note that the center of G2 is perfectly positioned in the East-West direction, and likewise the center of G3 is perfectly positioned in the North-South direction for the purpose. The more you move them, the less golden the rectangles. The contemporary academic consensus is that no Egyptians of the IV Dynasty were familiar with the Golden section. Tedder's analysis is not considered a proof due to the inaccuracies involved. Therefore, I'm really glad to be able to show total accuracy implicit in the plan. Perhaps, the academy will notice. |
| The
Golden Column The Golden Column, seen below, occurs naturally in the context of the Pyramid Square after a pentagram construction. It is a composite of two golden rectangles, one upright, one horizontal.  C divides A-K so that if C-K equals Φ - 1, then A-C equals Φ, and A-B equals 1. The length of the combined rectangle (the Golden Column) then is 2Φ - 1.) The diagram below shows two different Golden Columns, although we can only see one at this resolution. One is the exact Golden Column from the previous diagram, while the other, the Tedder's one, is set by the N-S distance between the pyramid centers. No doubling nor thickening of lines is seen between the columns on the outside. However, the western vertical side of Tedder's original rectangle visibly divides the entire column in a wrong place; it's 74 inches too long.  There is something in this diagram that turns on the proverbial lightbulb _ a line from the point 'O' on the Golden Column, made to be tangential to the Great Pyramid's inscribed circle, is at the same time a golden diagonal. Evidently, one can use this golden diagonal to reconstruct, with visual perfection, the Great Pyramid's square base as it relates to the Pyramid Square. The pyramid's side will then be shorter by over 6 inches, invisible on this scale. So, if we suppose that this was how the builders had evolved the Giza plan, it would be in agreement with Giza's sacred nature, because the Golden Section was always considered sacred geometry. The notion that this figure, the Golden Column, was sacred to Egyptians, is also supported by my analysis of a door from Hesire's tomb.. http://www.vejprty.com/hesire.htm The figure of Hesire engraved upon the door fits snugly into the same golden-column. Φ - the Second Nature of the Pyramid Square Yet another horizontal golden rectangle makes an appearance, exclusive to the context of the Golden Column within the Pyramid Square, as two pyramid lines seem to converge into a point on the golden diagonal emanating from '7', the northwestern corner of the Golden Column: 1) 'h' - extended eastern side of the Third Pyramid 2) 'g' - extended diagonal of the Second Pyramid rising northwest That the existence of this rectangle is not accidental is confirmed by its reappearance based on another method. (see the second diagram below) Although the two are not identical, they appear to be identical at this scale, with the latter rectangle being more accurate. 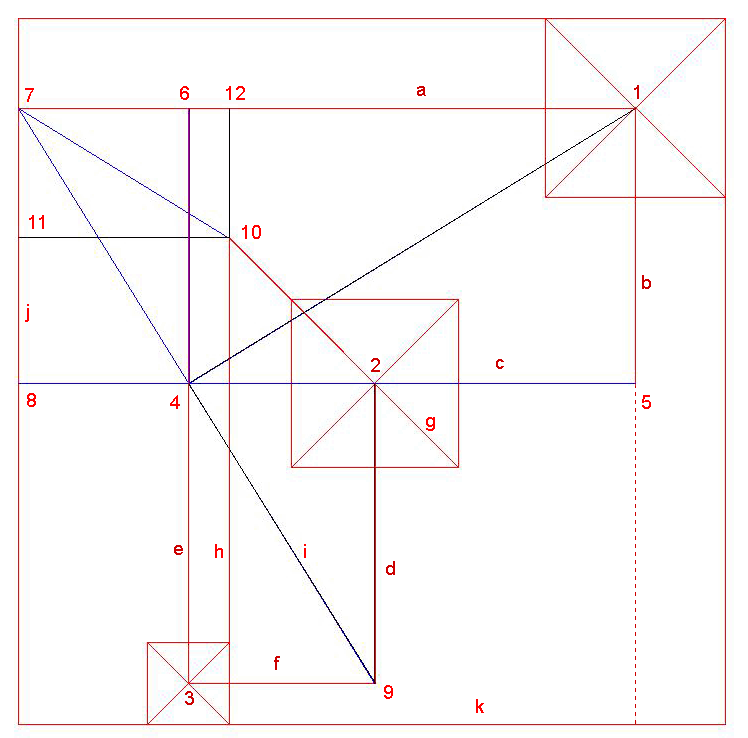 The second rectangle is an unintentional consequence of a separate idea proposed by Jim Alison: Quoting Alison: A 45° diagonal from the apex of the third pyramid intersects the SE diagonal of the first pyramid very nearly 220 cubits from the apex of the first pyramid. Thus, a circle inscribed inside the first pyramid very nearly marks the point on the SE diagonal of the first pyramid that is at a 45° angle to the apex of the third pyramid. This 45° diagonal line from the SE diagonal of the first pyramid to the apex of the third pyramid is divided by the SE diagonal of the second pyramid in the ratio of 11/10, as shown in the diagram above. The length of this diagonal is 1773 cubits, a close approximation of the square root of π x 1000. The EW distance between the apex of the first pyramid and the apex of the third pyramid divides the 45° diagonal by the golden ratio. /End of quote  My simplification of the above text: 1) A line (y) is drawn from the center of the Third Pyramid to the lower intersection of the Great Pyramid's NW-SE diagonal with its inscribed circle. 2) A circle (x) originates from the center of the Third Pyramid and extends to the vertical axis of the Great Pyramid. This circle divides the line (y) into a close approximation of the Golden Section ratio. Practical Exploitation for the Reconstruction Here is a Giza-puzzle classic - less obvious, yet more important, ideas hide behind an idea with a better visibility. In this case, immediately after restoration of the Great Pyramid to Petrie's specification, there are available three interim simulations of the Third Pyramid. The above Alison's idea works wonders with one of those - G3, version #2 This time, let the circle (x) divide the same line (y) by the Golden Section ratio exactly. Then it will intersect the golden diagonal originating from the northwestern corner of the Golden Column at the point (I) - located just 0.66 inch above the Second Pyramid's diagonal. The golden rectangle set by (I) is a seeming twin of the other rectangle we had identified there before. Later, when we discover another procedure which produces a point 0.66 inch off to the other side of the same diagonal, we shall have located this diagonal with total accuracy, because parallel 45° lines through the two points create a channel, whose axis replicates the true diagonal. If the point (I) is set by the intersection of the extended diagonal of G2 with the same circle "x", the horizontal rectangle I-J-K-L will still be an excellent facsimile of a golden rectangle. distance I-J divided by I-L = 1.6199 less than 2/1000 off the true Φ value Logical Continuation - Pentagram Construction  The initial observations had reminded me of the style of the creators of Nazca Monkey and the Athena Engraving. Those two masterpieces both derive from the construction of the 5-pointed star and emphasize the same unique method above the many available (the 13-step method). Therefore, I tried it out, and it worked just great. While all the other methods can be used to reproduce the initial Great Pyramid square base in relation to the Pyramid Square, only the 13-Step method of the star design automatically produces a point which accurately locates one of the sides of the Second Pyramid: to 4 mm or 1/6 inch north of its southern side. This is a key tidbit of information, as later on it lets us reconstruct the position of the southwestern corner of the Third Pyramid exactly as it's given by Petrie. Geometry First The reconstruction remains in the domain of pure geometry until the Great Pyramid stands exactly reconstructed in proportion to the total S-W span of the ground plan. The difference to Petrie's value is microscopic on Giza's scale _0.28 millimeter (1/100 inch)! Rounding like Petrie to the nearest tenth of an inch, the two designs are identical. A couple of imitation versions of G3, the Third Pyramid, also appears during this first stage. The second stage in the reconstruction of the ground plan of Giza also involves some significant cubit numbers in combination with geometry. Petrie's plan and its interpretation by Legon Petrie gives the plan like this: "The following are the Axial Distances in inches that separate the centres of the three Pyramids..." .................................................................N ..............................E ......... Centre of 1st to centre of 2nd Pyramid 13931.6 ..............13165.8 ....... Centre of 1st to centre of 3rd Pyramid 29102.0 ................22616.0 ......... Centre of 2nd to centre of 3rd Pyramid 15170.4 .................9450.2 ............. Petrie already gave the mean side for each pyramid; so we can reconstruct his plan from North to South. The total South to North distance of this plan is 35,713.2 inches. Now, in comes Legon who needs to duplicate the plan in an alternate way.. "From the above survey-data, we can now compute the major components of spacing between the sides of the three Pyramids, as follows:" Distances between sides from North to South Inches Cubits Design N 1st to S 2nd 22,703.4 1,101.04 1,101 S 2nd to S 3rd 13,009.7 630.93 631 N 1st to S 3rd 35,713.2 1,731.97 1,732 S 1st to N 2nd 5,159.7 250.23 250 S 2nd to N 3rd 8,856.1 429.49 429.5 The problem with the above is that the top two lines should add up to equal the third line: 22,703.4 + 13,009.7 = 35,713.1 but the third line = 35,713.2 Like Petrie, Legon is rounding his distances to the nearest tenth of inch. In Petrie's model, these distances between pyramid sides work out to being 0.05 inch longer. 22,703.45 + 13,009.75 = 35,713.2 However, it is very well possible that if Petrie were to state the plan in the same terms as Legon, he would use exactly the same values as Legon (values rounded to tenths of inches). Quoting Petrie: "A line of levelling was run from the N.E. corner of the Great Pyramid, to the S.E., to the S.W., up to the top, and down to the N.E. again. The difference on return was only 1/4 inch, or 1"-5, on 3,000 feet distance, and 900 feet height." By that standard, it is entirely feasible that Petrie was a tenth of an inch off the real value of the N-S span of Giza. Legon's Axial Distances between sides from East to West Inches Cubits Design W 1st to W 2nd 12,868.8 624.09 624 W 2nd to W3rd 7,289.5 353.52 353.5 E 1st to W3rd 29,227.2 1,417.42 1417.5 W 1st to E 2nd 4,393.9 213.09 213 W 2nd to E 3rd 3,135.9 152.08 152 The table above has the same problem. The value of the first two lines plus the 1st pyramid's side should equal the third line, but it does not. 12,868.8 + 7,289.5 + 9,068.8 = 29,227.1 But the third line is 29,227.2 In Legon's model the shortened gaps between pyramids add 1/10 inch to the combined length of pyramid sides, if the model equals the span of Petrie's Giza plan. The Basic CAD Model of the Ground Plan The basic model of the ground plan becomes our target which we try to reconstruct by mathematical procedures. For this target model I took Petrie's value for the mean side of the First Pyramid, and added Legon's value for the gap southwards between it and the Second Pyramid. To that I added Perie's mean side of the Second Pyramid, added the gap between it and the Third Pyramid, and added Petrie's mean side for the Third Pyramid. I used the same method going from east to west. 9,068.8 + 5,159.7 + 8,474.9 + 8,856.1 + 4,153.6 = 35,713.1 inches = 2,976.1 feet At the time, I was oblivious of the discrepancy of 0.1 inch between this version and Petrie's version since I had continued by immediately switching to cubits as units, counting the S-N span as 1732.05 cubits exactly. Thus, the discrepancy in inches was kept out of sight.. It was one of the luckiest mistakes I ever made! The reconstruction process had turned out absolutely perfect. Then I found out that my target model was actually a hybrid of Petrie and Legon models. True, a difference of a tenth of inch seems insignificant over the distance of almost one kilometer between the north and south edges of the Giza plan; and moreover, the size of each pyramid remains identical to the one given by Petrie; nonetheless, the position of the two smaller pyramids in Petrie's version shifts slightly in relation to the Great Pyramid - 5/100" for the Second Pyramid, and 1/10" for the Third Pyramid. Somewhat surprisingly, Legon's model at 35,713.1" is the one in ideal harmony with the inherent mathematical ideas _a harmony unachievable if translating 1732.05 cubits into Petrie's 35,713.2 inch value instead. What is one to think? What are the main arguments for the notion that the hybrid model is the correct one, if we suppose that there is indeed one such correct model available for discovery? Luxury of Being Documented - Global Mirroring of Ideas The Giza plan does not stand alone; it forms a geometric trilogy with: a) Approximately 15,000 years old, an engraved tablet from La Marche, France is hands-down the mathematical superstar among all drawings - this touchstone matters more than any other picture in the world. b) The Nazca Monkey from Peru duplicates the essence of the engraving from La Marche - it is the world's most important geoglyph. The development of both designs begins with the same unique method of pentagram construction, just like the Giza plan. The first major product of both the La Marche and Nazca pentagrams is the same uniquely positioned square. At Giza it is also a square, albeit a different one - the containing square for the three pyramids. Each of the three masterpieces finds ways to emphasise that its umbilical cord connects to the same pentagram construction. To-and-Fro Feeding of Ideas Since the trilogy stands on a common geometrical basis, we can experimentally transfer individual parts from one work to another to see if and how they fit there. I took the Giza ground plan and integrated it into the other two works. The result was a series of instances of a tailored fit between the plan and the images. Some invaluable insights ensued. Above all, the Great Pyramid looms dominant in the design of Athena's head, while the Second Pyramid also plays a large role. The pyramid is virtually Athena's head, and Athena's head is the Great Pyramid. What we have here is a valid historical document of an indisputable direct connection between the two. The document suggests that Giza's chief architect is a female who was around 15,000 years ago! More than just a revision, this a virtual upheaval in history * Length of the Royal Cubit Legon makes a strong case that the North-South distance between the pyramids was meant by the builders to equal 1.732 cubits, or 1,000 times the square root of 3. By my observation, they had meant it as 1,732.05 cubits, the square root of 3 given to an impressive five decimals. (1,732.05 squared = 2,999,997 - practically perfect three million.) This is also a strong hint that drawing the corresponding square might help us understand the position. . Petrie's measurements at Giza, and inside the Great Pyramid had produced slightly differing values for the cubit. In the end he had settled for an average of 20.62" ± 2/1,000 (inch) per cubit. This reconstruction's cubit is 20.618977...", in Petrie's range. North to South distance between the pyramids = 35,713.1 inches = 1,732.05 cubits = a side of the Pyramid Square 1 cubit = 20.618977512196530123264339943997 inches = 523.72202880979186513091423457752 millimeters It makes good sense for the designer to stop at the exact value of 1732.05 cubits (here is an example of a puzzle using decimals from La Marche, Stone-Age France ). This is a natural cut-off point as the digit 5 for hundredths is followed by a zero, which means no thousandths to deal with (1/1000 cubit is just over half-a-millimeter). The next digit represents an already too fine distance. As a representation of the square root of 3, our value differs from the true by eight ten-millionths of a unit - 1.73205080.. How to Recreate Petrie's Giza Ground Plan From Scratch part one The Foundation - Classic Geometry The Giza plan evolves from a solid theoretical foundation - the Golden Section, showcasing an elegant method of construction of the regular 5-pointed star. This method was brought to my attention by the Nazca-monkey glyph. 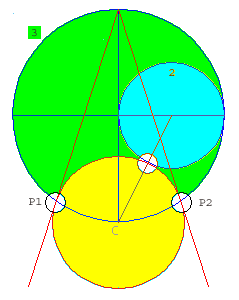 Diagram 1 Start with the above classic procedure. It begins with a horizontal line, the future horizontal arm of the star, and takes ten steps. Two of the steps involve help circles (to draw the axial cross), and these are not shown. The eighth step draws the key Golden-circle (yellow), which is centered in the bottom tip of the axial cross. On steps nine and ten, lines are drawn from the top of the axial cross as tangents to this circle (at P1, and P2). These lines create an exact angle of 36 degrees (like on a 5-pointed star). Before going on, this simple diagram already has two crucial elements: * The base of the golden triangle, given by the 36° angle intersecting the horizontal axis, is of the same length as one side of the Great Pyramid's prototype in this reconstruction.. * The circle from step 2 of the construction is the actual instrument which adjusts the prototype Great Pyramid to within ¼ millimeter of Petrie's plan. It shows the strong bond between this pattern and the reconstruction itself. 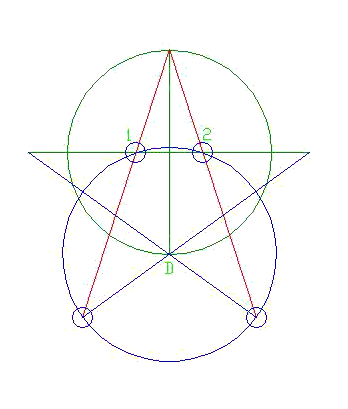 On step eleven, we have a choice of three points (D, 1,2) from which to draw a circle. The one shown above centers in "D" and passes through "1" and "2". Then the other two (circled) points at which the circle crosses the 36 degree angle lines mark two more tips of a regular 5-pointed star. Lines from those tips drawn through "D" then complete the star. In trade terms, the simplicity of the construction is 13. I was able to find one such construction on the web with the simplicity of only 12, but no other simplicity 13. The rest seem to be simplicity 14 and more. The other choices use the same circle drawn from either "1" or "2" in the above diagram.  Diagram 2 Golden Rectangles Galore The position below is based on diag.1, but is rotated 90 degrees counterclockwise. It contains a slew of golden rectangles.  Diagram 3 * A line from 'A' through '1' and on to 'D' has the angle of a diagonal in a vertical golden rectangle, hence 'ABCD' is a golden rectangle. * A line from 'B' through '1' is equivalent to a golden diagonal, as well. * A line from 'D' perpendicular to 'AD' is a golden diagonal in 'CDEF'. * The combined form of the two golden rectangles (ABCD + CDEF), the 'Golden Column', will be our key to setting the Great Pyramid's side to Petrie's value. * The Horizontal Column is next transformed into a square. One of the ways to do it is adding the golden circle's diameter to the underside of the column. * A 45° line drawn from 'H' will be one of the diagonals of the Great Pyramid. ' * E' - will be the center of the initial Great PPPyramid in our plan. A line through the points of intersection of the two golden circles in the diagram is yet another golden diagonal. The ratio of the Golden Column's height to the height of the rest of the square is 2(Φ-1). The points A-B-I-J-H mark four segments in a row, where each segment forms the Φ-ratio with the neighboring segment(s). Corners of the Great Pyramid's Prototype In the diagram below, on both the blue 13-Step star, and its derivative - the red star, distances such as 'AB', and 'EF', are equal to 'CD', a side of the initial Great Pyramid. At this scale, it is impossible to see any difference between the imitation, and the true-size Great Pyramid. The diagram shows one way of drawing the pyramid's print in the sand. A line-segment through 'P' and 'C' is the same as one of the diagonals in a horizontal golden rectangle; it rises to 'C' to meet the left-rising diagonal of the initial Great Pyramid at the pyramid's northwest corner. The segment is also key to further construction. The green square's extended side crosses a line of the red star at 'X'. This point is only 4 mm north off the southern side of the Second Pyramid.  Diagram 4 ___________________________________________________________________________________ Lines a, b, c, d all have the golden diagonal angle. In the diagram below, three of the four - 'a', 'b', and 'd' project the Great Pyramid onto the "13-step" construction. Line 'b' is tangential to the inscribed circle of the pyramid, and that also permits the reconstruction. This is the only generic way I know of to construct the initial Great Pyramid. Every other way has to do with the 13-Step star.. Line 'a': As the radius of a 'transmission circle", it will usher this reconstruction from theoretical to applied stage when its turn comes. Line 'b' measures 1642.00222202 cubits, a calibrated measurement, typical for this reconstruction.  Diagram 5 Diagram 5In the diagram below: One Q-circle intersects sides of the diamond (square); the other one intersects extensions of those sides. Lines 'e'and 'f' originate from these intersections, and then intersect the initial pyramid's diagonals at its corners Either 'e', or 'f' suffices for the pyramid's construction. Altogether, there are five procedures, each projecting the same initial pyramid. Only one is generic, the others are connected to the 13-Step construction. The design's nature is itself a strong hint at the designers' familiarity with the entire spectrum of possibilities therein. If the designers had known only the single generic way to project the initial pyramid, the incentive for selecting it at all would be much diminished.  Diag.6 If the NE corner of the initial Great Pyramid (G1) is exact in this blueprint, the other corners are over 6 inches short of Petrie's locations. Yet, that distance shrinks to an invisible nothing on any drawing board ( 1/100 millimeter, if the board is 35" tall). The North-South division - Location of the south side of G2 The point marked 'X' in the above and below diagrams sets a point on the south side of the initial Second Pyramid (G2). If the height of the big square is Giza's 907,115.28 millimeters, then 'X' is 4.2 millimeters above the south side of G2, as given by Petrie. Without the '13-Step' star there can be no point 'X' - key to the best result in locating of the Third Pyramid's SW corner (to 0.51 mm). The length of a side of the initial Great Pyramid, as well as a side of the pentagon within the 13-Step Star, is the remarkably precise 439.5000... cubits. It's a strong signal that the units used are correct. The distance between adjacent tips of the 13-Step star, or one side of the smaller star = 1150.626180 cubits. Remarkably, that's five consecutive digits of Φ squared (2.6180).  Diag.7 The Pyramid Square After the initial pyramid (proto-pyramid), the big square in diag.3 is extended to the pyramid's north-east corner to function as a containing square for the pyramids - the Pyramid Square (35,713.1" or 1,732.05 cubits per side). How to Recreate Petrie's Giza Ground Plan From Scratch part two Follow the Illusions The Giza layout is uniquely expressive by being really close to an unprecedented number of elegant ideas which might have dictated its design. One by one, these turn out to be inaccurate, mere illusions. Yet, at least at Giza, illusions are part of reality. Like in stereoscopic vision, separate illusions merge into the real thing. All one has to do is get on the right track, and Giza designers provide further guidance in the form of pictorial clues, special effects. It doesn't take long to the first exact reconstruction of one of the pyramids in the context of the Pyramid Square, and it is the Great Pyramid. Illusion #1 - Draw a circle from the southeastern (bottom right) corner of Giza's containing rectangle, such that it touches the Great Pyramid's circumcircle. This circle creates an illusion in that it also touches the southeastern corner of G3 (Menkaure). Illusion #2 - The same circle appears to be of the same size as the "Transmission-circle" in the diagram below, whose radius is the golden diagonal from the pyramid's NW corner, marked as "a" in diag.5. So, we copy the Transmission-circle to the bottom right corner of the containing rectangle, as well. When concentric, the two circles merge into a single circle on this scale.  diag.8 Illusion #3 - From the center of the imitation Great Pyramid, draw a circle, which touches the Transmission-circle, then copy it to the southwestern (bottom left) corner of the Pyramid Square. It gives the illusion of touching G3 from the other side (diag. above). This is certainly a startling effect, albeit up close it is not all that accurate. So, we have two pairs of alike circles , which look the same when the entire Giza is in view. Without viewing things in the context of Pyramid Square, we would be deprived of this interesting observation. Illusion #4 - Another special effect is shown below. Line 'g' drawn from the left intersection of the two Transmission circles to the SE corner of the initial Great Pyramid then duplicates the golden diagonal angle to 0.0015º. The true golden diagonal drawn from the same point approaches the same SE corner to within 0.66''. Should we overlay this diagram with diagram 5, line 'g' would be indistinguishable from line 'd' in diagram 5.  Menkaure's initial vertical axis ('go down the middle') The midpoint of the gap between the Transmission circle and its complement circle sandwiching G3 is 4.2 inches to the west of Petrie's vertical axis for the pyramid. The vertical axis of our first version of reconstructed G3 is drawn from this midpoint. The First Mock-up of the Third Pyramid (#1) a) * Center a circle at the point, where this vertical axis crosses the bottom line of the Golden Column, also the central axis of the original mother star, the 13-Step star. * Have the circle touch the far side of the original imitation pyramid (marked 1) centered in the column's SW corner. b) The section of G3's vertical axis below the new circle is taken as equal in length to the sides of G3. That is all the data needed to complete this pyramid. Its sides are 6.1 inches shorter than the original. The left side is just 1.2 inch to the west of the original. All in all, this is a pretty good imitation of the original.  diag.12  Consistency of the Method The method of creating the first imitation of G3 is consistency itself. It bases on the same visual effect - a circle touches either a pyramid side, or the circle described around a pyramid. The Benefit Having the first imitation of G3 gives a choice of three immediate actions: 1) approximate one of G2 diagonals to 0.66" 2) improve the accuracy of the first imitation of G3, i.e. create a second version of G3 3) this first version of G3 becomes an instrument enabling a simple operation in which we duplicate the Great Pyramid exactly as specified by Petrie. In other words, it is a gamepiece created to continue the planners' game. The Second Version of the Mock-up of the Third Pyramid (#2)  In a variation of the above diagram, we have the Transmission-circle and its look-alike circle again, but this time its look-alike circle is tangential to the circle around the prototype Great Pyramid, rather than the true pyramid. In the magnified detail view below, 'a' is the Transmission-circle, and 'c' is its look-alike circle. Lines '1' and '2' show the southeastern corner of G3 as given by Petrie. The midpoint between 'a' and 'c' becomes the southeastern corner of the # 2 mock-up of G3. It is 3.68 inches to the west of the true corner. The southwestern corner remains the same. A pyramid side in this version is 2.509 inches shorter than the true side - an improvement over the first version.  Operation Rising Column Robin Cook says that if we enclose the pyramids between 45º lines perpendicular to their N.W. by S.E. diagonals, as in the diagram below, the long axis of the resulting rectangle (the Rising Column) is almost exactly the same as one of the Second Pyramid's diagonals.  diag.
13 diag.
13The axis actually runs 13.82 inches east of the pyramid's diagonal; however, this relationship does look exact on computer screens or paper. I noted something three times more accurate in this position : the width W-Z of the Rising Column is just 4.32 inches more than the width A-B of the Golden Column. The two could switch places and one wouldn't know it from just looking. The idea is intriguing; experimentation is in order. The illusion that the bottom side of the Golden Column is identical with the horizontal axis of Khafre's pyramid (G2), is a 10.12 inches miss. However, marking the actual on-the-ground thickness of the Rising Column downward from the top side of the Golden Column gets to 0.94 inch south of the Second Pyramid's horizontal axis. The idea is intriguing; experimentation is in order. The "Channeling" Method of Reconstruction Given two possible approximations of the original which form a channel of parallel or concentric lines, sometimes the solution is simplicity itself: their average. "Sail the middle of the channel!" Exact Duplication of the Great Pyramid Place a copy of the Golden Column, axis over axis, over the Rising Column (using the first version of G3). The situation in the Great Pyramid's NW corner now looks like the following diagram.  diagram 14 A line drawn vertically down from the northwest corner of the wider Rising Column becomes one with the western side of the Great Pyramid in Petrie's version. Or, we can use the axis of the channel between the western sides of the two rising columns. It is identical to the western side of the Rising Column as given by Petrie. The difference in length between the reconstructed and the original versions of one side of G1 is too tiny to pay attention to, at 0.01 inch, or 0.28 millimeter. In other words, the two versions of the Great Pyramid are identical. Our value: 439.827 (439.8273..) cubits, or 9,068.8 inches ( 9,068.81501...) per side. 439.82732 / Pi = 140.001.. Petrie's value: 439.828 (439.8278..) cubits or, 9,068.8 inches Our value is actually a hair closer to the optimal value of 439.823 for Pi encoding. Pi times half the pyramid's height = 439.8229.. or, 439.823 rounded Consistency and Versatility of Method The very same procedure works in the diametrically opposite corner of the Rising Column, albeit not as well, as it locates the SE corner of G3 to 0.5". This is version #3 of the initial G3. its sides are now 0.66897634 inch longer than Petrie's original (the SW corner remains the same). More versions are still ahead.  diagram 14b In the diagram, 'a' and 'b' are sides of our first imitation of G3, and 'c' is the new reconstruction of the eastern side of G3. The line "c" in this third version is an obvious improvement over the first two versions.. ___________________________ Very Special Effects diagram 10 Coincidences around the Transmission-circle certainly make it important. The line segment which we took for its radius also has some big points on it in the context of the '13-Step' construction (diagram below). Point '2' is a big point in the original 13-Step-star's construction, a corner of this star. The segment 3-4 duplicates the golden circle's radius from the same construction.  diagram 11 One of the Accurate Reconstructions of the SE corner of G3 With the Great Pyramid duplicated, it is now possible to do the following:.  diagram 8 Diagram 8 shows the situation in the SE corner of G3, Menkaure close-up . Lines '1' and '2' belong to the pyramid as given by Petrie. 'a' which looks like a straight line in this magnification is the Transmission-circle 'b' is the tangential circle to the duplicated Great Pyramid's circumcircle. The circles are spectacularly equidistant to the pyramid's corner: The axis of the channel between them is 0.13 inch, or 3.1 mm to the east of Petrie's corner. The distance between the aforementioned circle-lines then works out to 2.0010 cubits. This result is the closest I managed to get to Menkaure's SE corner by pure geometric construction, without resorting to units. This gives us Version #4 of G3. The same process using the Great Pyramid's circumcircle, as given by Petrie, gets us to 3.4 millimeters off to the east of the pyramid's corner..  A number of other ways (version 5) The radius of the cyan circle, between lines 'a' and 'b' in the diagram is 1.0005.. cubit, a very accurate reading at only ¼ millimeter off the whole number 1. Measuring one exact cubit eastwards from the tangential circle reaches 2.85 millimeters east of the SE corner of Menkaure, 0.25 millimeter closer than the geometric method. This goes well with Legon's observations of Giza's attributes in whole cubits. 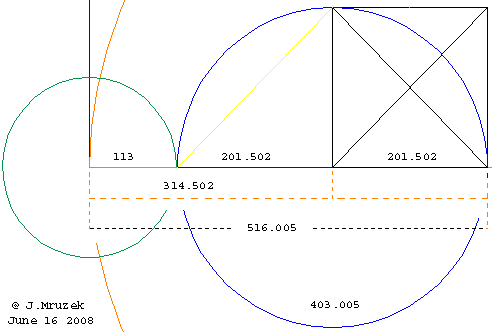 diag. 15 The location of the prototype SW corner of G3, the third pyramid, yields some remarkable readings in cubits. The distance from the SW corner of the Pyramid Square to the SE corner of G3 is: 516.005 almost exactly 516. (version 6) a) So, if we measure 516 cubits exactly from the SW corner of the Pyramid Square, we'll be some 2.5 millimeters short west of Menkaure's SE corner. Now, recall the result from above: "measuring one exact cubit east from the tangential circle comes to 2.85 millimeters east of the SE corner. The two results average out to 0.175 millimeter (1/6 millimeter) east of the SE corner. b) The first imitation southwestern corner of G3 in combination with the real southeastern corner of G3 is accurate to 0.00246 cubit (a little over one millimeter) to what many authors posit to be the intended side of G3 : 201.50246 or 201.5 cubits (version 7) Thus, going 201.5 cubits eastwards of the imitation SW corner gets to 1 millimeter west of its SE corner. c) The distance between the prototype SW corner of G3, and the SW corner of the Pyramid Square: 314.5 0275 The above 201.50246 and 314.50275 have very similar fractions: 314.50275 -201.50246 = 113.00029 Put into words, if we flip over westwards the distance between the prototype SW corner of G3 and Petrie's SE corner, it is short of the SW corner of the Pyramid Square by: 113.0003 cubits, which is just 1/6 millimeter short of being perfect 113 cubits. Exact Reconstruction of the Third Pyramid's SE corner * Mark exactly 113 cubits from the SW corner of the Pyramid Square toward the SW corner of G3. * The remaining gap to this SW corner of G3 becomes the radius of a circle centered in the same corner. This circle then locates the target SE corner of G3 to within the above mentioned 1/6 millimeter, or 0.0003 cubit east of Menkaure's SE corner. In plain English, the two locations are perfectly identical. Noteworthy: Do you recall this tidbit from above? <the two results average out to 0.175 millimeter (1/6 millimeter) east of the SE corner of Menkaure> Hence we have two ways to get the same result for Menkaure's SE corner - each 1/6 millimeter east of that corner. Precise location of Menkaure's SW corner Once we know the exact location of Menkaure's SE corner, we can also locate its real (as given by Petrie) SW corner, thanks to a brilliant idea of Legon; I presume it's his because he cites no sources for it.  Draw a square 555 cubits per side, as in the above diagram. Inscribe a circle with the radius of 250 cubits and draw a tangent line parallel at 45 degrees. You obtain an exact half base of Menkaure, the Third Pyramid, which is easily completed into a whole square whose sides then come to 201.446 cubits, or 4,153.6 inches long, exactly as specified by Petrie. This is as simple as it is brilliant, and it is yet another glimpse of Giza plan's theoretical depth.   |
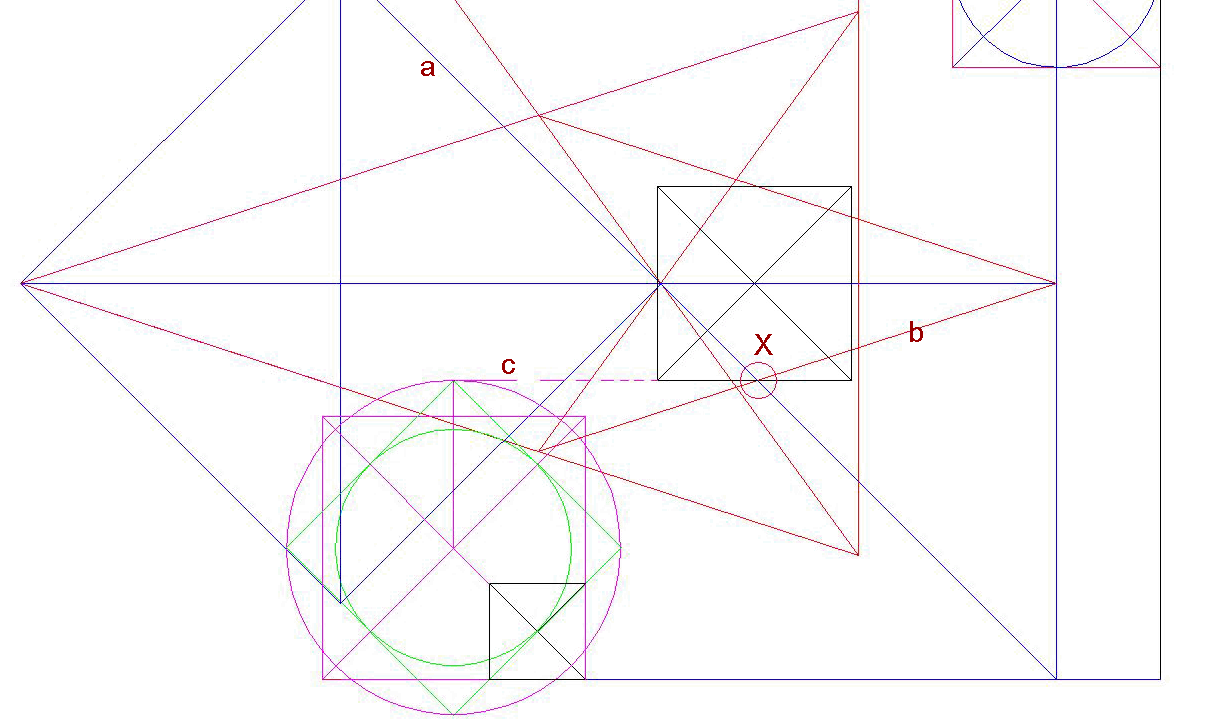
| With one corner of the
third Pyramid already located, we apply the same method
from there and reconstruct the pyramid, as in the diagram
above. It's as simple as that. The new design blends
into the old nicely, namely, the green circle and the
green square. There is another way to reestablish the Third Pyramid exactly to Petrie's specification, but to do it, we have to wait until we get to pinpointing the center of the Second Pyramid later. It too, is Legon's idea, but we do it our way and get a closer result than Legon. Hints at Pi (π) and the Golden ratio (φ) Once we draw a circle with the radius of 113 cubits from the Southwestern corner of the Pyramid Square, there is an incidence of what seems to be hints at π and φ values on both sides of it. The distance from the circle to the western side of G3 is 314.5 cubits. Numbers 113, and a 314 together evoke a widely known Pi approximation. 355/113 = 3.141592.. The distance from the circle to the adjacent corners of the Pyramid Square is 1619 cubits. 1732 - 113 = 1619 is just 1 off Golden Ratio's 1618 1618 rounded to three digits is 162 _ φ rounded to three digits. 1619 rounds out to 162 _ φ rounded to three digits. The speed of light in nautical miles is 162,000 More specifically, it is: 161874.977 which rounds out to four digits as 1619. | 1732 - 162 = 1570 ...... 157 x 2 = 314 (π digits) The Legon's construction dealt with above divides the 555 cubits long side of a square into 250 x √2 and 201.446..., the latter being the side length of G3. 250 x √2 = 353.55339... 355 and 339 are in sequence 353.55339 - 39 = 314.55339 It is 314.50275 from the initial SW point of G3 to the SW point of the Pyramid Square. The difference between the two is 0.050... cubits, 2.5 millimeters, or 0.1 inch 355/339 = 1.047197640 = π /3 because: 1.047197640 x 3 = 3.141592 ....... the first seven digits of π Pi, Golden Ratio, and speed of light are recurring topics in Giza discussions. Reconstruction of G2 (Khafre, the Second Pyramid) First, we need to locate the SE corner of G3 for the exact reconstruction of the Rising Column. Then, marking the width of the Rising Column (W-Z), downwards from the top side of the Golden Column, gets to 0.94 inch south of the Second Pyramid's horizontal axis'. Although this is a nice approximation for the horizontal axis, its true function is to help us locate the vertical axis of G2.  diag. 13
diag. 13G2 - diagonal simulation # 1 - Channeling" the Solution Jim Alison had read the position in the diagram below, as saying that a circle centered in G3, whose radius is the horizontal distance between the centers of G1, and G3, closely approximates the Golden Cut in the given line (the green line marked Phi). The line is also very close (0.8º) to holding the 45º angle with the horizon. The circle divides it rather nicely in the Golden Proportion: 22,616 inches / 13,954.114 inches = 1.621  However, with the golden diagonal emanating from the Golden Column's northwestern corner in the picture, an interesting visual effect occurs - the golden diagonal, the Second Pyramid's extended diagonal, and Alison's circle all seem to meet in a point. It is an invitation to experiment like in the diagram below: 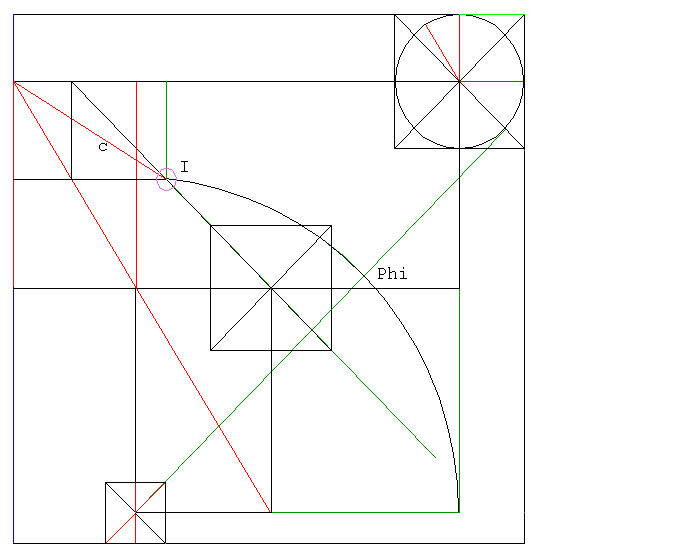 This circle intersects the golden diagonal "c" at "I" in the diagram. The point "I" simulates a point on G2's diagonal. This relationship is an order of magnitude more accurate than the one Alison noted. The simulation falls 0.66 (0.6592..) inches northeast off the original. Note: This method works this well only with #2 version of G3. G2 - diagonal simulation # 2 Two major lines: 'a' - the axis of the initial Rising Column (it was the key to Great Pyramid's duplication) 'b' - the bottom line of the Golden Column meet 0.66 (0.664..) inch southwest of the diagonal 'd' of the pyramid in Petrie's plan. This creates a point of insertion for the diagonal simulation 'c'.  diag.
17 diag.
17The channel axis 'd' between the two diagonal simulations (lines 'c' and 'e' in the diag), runs 0.0001 cubit, 0.003 inch, or 0.07 mm southwest of the diagonal given by Petrie.. It is truly identical to Petrie's diagonal. The line 'c' is a dual purpose line; it combines with yet another major line to pinpoint the vertical axis of G2. *** A Repeat of the Column Substitution Idea - the Second Pyramid's Center Located The Golden Column substituted for the Rising Column lets us duplicate the Great Pyramid as specified by Petrie. Now, the same trick works in reverse! The Rising Column in its final form suspended from the the top line of the Golden Column, falls 0.94 inch south of the second pyramid's horizontal axis (cyan in the diagram below). This line simulates the axis nicely, but its true purpose is different. It meets line 'c', the Diagonal Simulation #2, 14/10,000", 35/1,000 millimeter, or 7/100,000 cubit east of Petrie's vertical axis. Those are mighty fine specs. Considering the size of our work-space, Giza, expecting this kind of results would be far from realistic.  diag.18 diag.18 The axis and the diagonal together locate G2's center a pinpoint away from Petrie's plan, at 0.005 inch (1/200"), 0.13 millimeter, or 0.00025 cubit. We know the position of G2's southern side to 4 millimeters since the very beginning; therefore, the Second Pyramid can be recreated with impressive accuracy even before its final adjustment. An alternative exact way of reconstructing the Second Pyramid's NW-SE diagonal Having two or more perfectly adequate ways of accomplishing the same task is a pure luxury, yet it is a reoccurring motif in our reconstruction. It is clearly systematic.  The big red circle in the diagram is actually double, with centers in both the #2 and #3 versions of G3: From the pyramid-center of each version, draw a circle through the SW corner of the Golden Column. Each circle seems tangential to the same axis of G2. In fact, both come close. G3 #2 version - the circle is 0.8286 inch short of the axis, while in G3 #3 version - the circle is 0.8163 inch past the axis. The axis line of this channel is 0.006 inch, 0.0003 cubit, or 0.16 millimeter to the southwest of the original G2 axis given by Petrie. Since we already have a point just 4 millimeters above the south side of the Second Pyramid, the pyramid can be completed as the initial Second Pyramid. Its sides will be over 8 millimeters shorter than the true pyramid, extremely close, but still not perfect. Its center and diagonals are ideal, however. the Third Pyramid - Final adjustments Having the initial Second Pyramid permits testing Legon's ideas in our settings. The size of the pyramid is determined by using the point (x) from diagrams 4 and 6, a little over 4 millimeters closer to the center. 1: The east-west distance between the west sides of the Second and Third Pyramids equals 250√2 cubits. This postulate locates the west side of the Third Pyramid 0.006 cubit (3.45 millimeters) west of Petrie's version. 2: The east-west distance between the center of the Second Pyramid and the west side of the Third Pyramid equals 250√2 + 205.5. This postulate works even better, locating the west side of the Third Pyramid 0.003 cubit (1.5 millimeters) west of Petrie's version 3: Counting 250√2 + 411 cubits westward from the east side of the Second Pyramid does finally locate the west side of the Third Pyramid, as it locates its SW corner 0.0014 cubit (0. 5175 millimeter) east of Petrie's specification. The other corner of the south side is given with an even greater precision, hence the Third Pyramid stands recreated exactly as given by Petrie. (This formula also works nicely for Legon's reconstruction - to 0.01 cubit (5.4 millimeters) east of Petrie's version.)  Diagram 19 Diagram 194: Working with the Pyramid Square confers an opportunity to note another Legon-style formula for the reconstruction. Draw line 'd' eastwards from the SW corner of the Pyramid-Square to the length of 250√2. Then subtract 39 cubits from it. The new segment ends 3.32 millimeters west of the Petrie's SW corner of G3. Segments 'b' and 'd' have a horizontal overlap of 0.00026 cubit, 0.005 inch, or 0.13 millimeter! This is more support for the validity of both the Pyramid Square concept and Legon's observations. We have counted five accurate ways to deploy an exact formula using 250√2 towards locating the SW corner of the Third Pyramid. So which solution should we use? The fact is that there are at once five accurate solutions for the west side of the Third Pyramid, or its SW corner. All are accurate - since Petrie's points come with a ± radius. We may think of those points as small circles, and all five solutions fall inside those circles. Multiple solutions designed into the Giza puzzle show off its sophistication. We shall never learn, which version was the one actually implemented on the ground. the Second Pyramid - Final Adjustment Draw a line 250√3 , or 433.0127.. cubits long westwards from the vertical axis of the duplicated Great Pyramid. Make this the distance to the east side of the Second Pyramid. The fault from Petrie's version then is 0.00126 cubit, or 0.66 millimeter. Since the center of this pyramid is already located with utmost precision, the adjusted Second Pyramid is identical in size to that given by Petrie. Conclusion: Petrie's layout of the great pyramids of Giza can be accurately recreated from scratch on a clean slate, beginning with the '13-Step' construction of the regular 5-pointed star from a line segment, with some involvement of the basic prime number square root values. The method has simplicity, total accuracy, elegance, and intellectual depth. With such attributes, it must be essentially identical to the actual procedure of planning the Giza layout. It is noteworthy that the method does not work with the classical tools of geometry, at least not without a microscope. Given the scale of Giza, and the tiny differences between drawing objects, the plan had to be worked out mathematically because the tiny differences could not possibly be seen and worked with on even the largest drawing board. The knowledge of mathematics guarded by the temples was clearly on a level unattainable in a neolithic society less than two millenia removed from the hunter-gatherer stage. Asked beforehand, if a microscopically exacting solution to the Giza ground plan were possible, I would have naysayed it, for even if there were an overall plan based on exact ideas, and it were executed flawlessly, it would not be possible to measure the perfect result accurately enough. This would have given rise to discrepances. Yet, we see such a solution here. I still see it as somewhat inexplicable, for no matter how good Petrie was, he himself assumed a greater margin of error in his measurements. Of course, my theory about the Agency would explain many things, but a discussion of the Agency is not an object in this article. ©Jiří Mrůzek April 15, 2007 Vancouver, BC last edited September 21, 2022 Notes Up to now, the academia has never accepted a single argument for the existence of advanced ancient science. Accordingly, a skeptic will say that even if Giza's ground plan could be cleanly translated into a sophisticated mathematical design, it would still be just one's own plan, nothing more than coincidence. It is established once and for all that our modern civilisation is the only highly advanced civilisation ever on this planet; and the Ancient Egyptians just weren't yet at the required level of mathematical knowledge. Of course, such reasoning is specious; there are lots of reasons why one should not consider the issue closed; and the reader is probably familiar with most. In passing, let me just mention a virtual mountain of material evidence for the presence of advanced technology in our remote past - super-heavy stone objects impossible to move by low-tech means. The Serapeum in Abydos is a perfect example of that - the cramped space in the Serapeum obviously rules out usage of massed work-force to move the heavy stone blocks involved. There is no room there to operate with levers or pulleys, and so on. Generations of professors of physics, engineers, and other experts had failed to explain how to accomplish such tasks by primitive means. Such a state of affairs leads to two conclusions: either the intellectual capacity of humans has substantially degenerated to where our best brains prove moronic in comparison to those of several millennia ago, or such tasks can indeed be accomplished only by powerful machinery. Cognitive Dissonance In effect, the academia seems to uphold the first option, which indicates that it is afflicted by collective cognitive dissonance. I add this opinion to my report as I'm editing it for the umpteenth time. It is late June, 2020 and times have been changing at a breakneck pace for some years, enough so as to deflect public attention from a tremendously important event having a direct confirmation bearing upon this narrative, because it is as good a proof of unknown technology superior to anything humanity owns up to, as it is an example of a truly outrageous case of world-wide cognitive dissonance. After seventy years of denial the American government discloses that flying saucers are real! They aren't called UFO's anymore; they are UAP's now. Instead of 'flying objects', they are 'aerial phenomena'. The former term is strongly worded; it is alarming and could cause public panic, lest the authorities are projecting their own fears, of course. One of the dictionary definitions of aerial is 'lacking substance'. The latter is relatively easy to swallow; it lets people cling to their outdated beliefs. In 2019, the American Department of Defense admitted that the US Navy videos leaked in 2017 are real. https://en.wikipedia.org/wiki/Pentagon_UFO_videos The disclosure was not followed by panic. Although the videos are just fragments of the available footage taken, they are true game changers. Though seventy years overdue for the countless people pilloried on the 'altars of science' over being branded in one way or another with the stigma of treating the issue of flying saucers seriously - this paradigm shifting disclosure opens a slew of possibilities. For instance, it validates the numerous reports of Foo Fighters by WWII pilots. Those describe the same flying saucers and the same capabilities. Our technology has advanced by leaps since then, but not the UFO's. They seem to be perfect, at the ultimate stage of their technological development. If so, how long have they been at that level? Thousands of years? Millions? By any measure, they don't fit the general tempo of evolution on this planet; therefore, they are unlikely to be from this planet. How long have they been here? Without going into details, historical sources indicate that they could be here as long as the human kind. Would it not be cognitive dissonance if I didn't recognize that since the UFOs' existence now stands on firm ground, there emerges a strong candidate for the explanation of many seemingly inexplicable mysteries from prehistory and ancient history? The American government has incontrovertible documentation of flying saucers. It is documentation of their presence and nothing more. In contrast, the three sites of La Marche, Nazca, and Giza document high-tech encoding of sophisticated mathematical themes into supposed primitive art. Conveyance of thought through geometry is a form of communication akin to writing. All that was served to us in the form of solvable puzzles. Who could be playing such a fantastic game with us? The civilisation behind the flying saucers is the only bona-fide qualifier for the candidacy. It makes my discovery that much more more attention-worthy. Measuring Success - Precise Values The reconstruction succeeds in duplicating the Petrie given sizes of the pyramids. Another aspect of the reconstruction which puts it into a class of its own is the undeniable extreme proximity of many of the resulting measurements to whole or half cubits. Distances given in cubits. 622.009.. a diagonal of the exact duplicate of G1 439.5000.. a side of the initial G1 411.007 a side of the initial G2 201.50.. a side of the initial G3 - less than 3/1000 from being a perfect half cubit 516.005.. from the reconstructed SE corner of G3 to the SW corner of the Pyramid Square 1787.5005.. distance between the centers of the duplicate of G1 and a version of G3 1642.0022 line 'b' ( diagram 5) 314.5027 from the reconstructed SW corner of G3 to the SW corner of the Pyramid Square -201.5025 from the reconstructed SW corner of G3 to the SE corner of Petrie's G3 = 113.00029 250√2 - 39 from one version of the SW corner of G3 to the SW corner of the Pyramid Square 2.001.. difference between the radii of the transmission circle, and its lookalike (diagram 5) 1150.626180 distance between neighboring tips of the Mother-star, five consecutive digits of Phi squared 439.82732 side of the reconstructed G1, which yields a very good value for Pi ( 3.1416..) with half-height of the pyramid (140 cubits) 439.8273 / 140 = 3.1416.. Mike Ivsin's own 14-step construction of the regular pentagon In my internet search, I came across some 15-step operations, but then in February of 2010, I got a letter from Mike Ivsin about his original construction of the regular pentagon. Applying Ivsin's ingenious original idea to pentagram construction, I found that it is a 14-step process. In the below diagram, the first five steps are in black color, the following five are blue, and the rest are red. Two of the circles appear as Vesica Pisces in order to clean-up the image.  Magic happens, when Ivsin goes on to add just one circle ('c') to the basic construction, whose radius equals the length 'a' of the star's arm (diagram below). Now, extend line 'b' so it meets 'c', and draw the line 'd'. What we have here is the cross-section of the Great Pyramid!  The angle between lines 'e' and 'd' is 51.82729237 degrees, which rounds out to 51º50'. A quote from Petrie: "On the whole, we probably cannot do better than take 51º 52' ± 2' as the nearest approximation to the mean angle of the Pyramid.. " * Hence, 51º50' complies to the lower ± limit set by Petrie. * The ratio of 'd' to 'e/2' is the exact value of φ (Phi). This is better than the usual Phi formula for the Great Pyramid: 356 / 220 = 1.6181818 The Giza layout, as well as the Great Pyramid's cross-section seem derived from Golden Section designs. Giza broadens the Nazca - La Marche connection (between the Nazca-monkey, and one Stone-Age engraving from the rock shelter of La Marche, near Lussac-les-Châteaux, France, with 1,500 masterfully engraved stone tablets, now kept in museum vaults, and largely unknown to the public). Why do these three ancient works separated by ages and continents encode the same construction? There is also a connection here to the apparent imagery of the so called Abydos Helicopter, which encodes yet another rigorous construction of the Golden Ratio. Petrie's value of 9,068.8 inches, or 230.348 meters, or 439.82782340 cubits of the actual average side by the standard of this study, is about 2.5 mm off the desired perfect value for Pi. An error of less than 3mm was allowed for by Petrie. Hence he could be off by that much, and the pyramid may have been built perfect. If we let the facts prevail, the conclusion must be that the average pyramid side was designed with the true value of Pi in mind. John Legon writes: "In terms of the Giza royal cubit of 0.52375 metres, the actual mean side of 230.364 metres corresponds to 439.8 cubits, with an average variation in the sides of only 6 cm or 0.1 cubit. Petrie suggested that an adjustment may have been effected in order that the perimeter of the base should express the so-called 'pi-proportion' in relation to the height of 280 cubits, with greater accuracy than the value for pi of 22/7. In this case, the theoretically exact mean side-length would be 439.822... cubits. It seems that the builders achieved this result while retaining the round number of 440 cubits in the south side."Naturally, a measurement dictates both its exact, and rounded out values. The need for a side of 440 rounded out cubits arises from the perspective of Phi. The apothem divided by half the side, or 356/220 equals Phi to the first three decimals (1.618 181818...) Mike Ivsin's construction produces perfect Phi, with a slope, which is in Petrie's ± range. It seems that the builders had achieved this result, too. Legon abstracts a cohesive system from the Giza position, one dealing with square roots. Although some of these readings are somewhat approximate, Legon suggests logical reasons, why there were adjustments. In my opinion, Legon correctly identifies an additional layer of abstraction in the position. Compared to the "13 Steps" reconstruction, it is considerably less accurate, yet it makes perfect sense in a rounded-out way. The more meaning, the more reason for selection of this plan. By the way, Legon seems somewhat unhappy over the east-west distance spanned by G1 and G3, which is 3 cubits too long to express the square root of 2 as 1414. Did he discount the fact that the north-south distance between the centers of the same pyramids is three cubits shorter than the desired distance and thus produces a correct average? east of G1 to east of G3 in my reconstruction = 1,417.. cubits north to south distance between centers of G1 and G3 = 1,411.. cubits The average of these two distances between these two pyramids is 1,414 cubits - the first four digits of the square root of 2. It is arrived at in a straightforward manner _ no numerology involved. These two distances between G1 and G3 also add up to 2828.. the first four digits of the square root of 8, which equals 2 x the square root of 2. These two distances between G1 and G3 also add up to 2828.. the first four digits of the square root of 8, which equals 2 x the square root of 2. It is interesting, because in this case the following formula is true: the square root of "a" cubed equals two-times the square root of "a". * A long-time researcher, Robin Cook adopts the right approach in observing all strong relations as possible coincidences first, and then asking, which of the mutually exclusive relations might be the intended ones. Cook is right, because without the illuminating background of the 'Pyramid Square', such ideas are a bit like Plato's shadows dancing on a cave wall. In such situations it is easy for a theorist to become convinced that his recreations mirror the Egyptian planners, before the builders strayed from the plan somewhat, just as expected, or before the plan got changed for reasons unknown. Considerations of Accuracy A quote from Petrie:"The probable error is an amount on each side of the stated mean, within the limits of which there is as much chance of the truth lying, as beyond it; i.e., it is 1 in 2 that the true result is not further from the stated mean than the amount of the probable error. If the glass is half empty, 1 in 2 (fifty-fifty) results will exceed the stated mean error. The excess is still most likely to be very close to the mean, because the odds against increase exponentially with distance from the true result (see the quote below). And since the glass is half full, half of Petrie's measurements should be be 1/10", or more, off. Quote: "Outside the Pyramids all the measures were ascertained by triangulation from the measured baseline of the survey; the first class points being fixed with a probable error of ±*o6 inch. The base of the survey was thrice measured, and is known with a probable error of ±"03 inch, or 1 in 200,000. A line of leveling was run from the N.E. corner of the Great Pyramid, to the S.E., to the S.W., up to the top, and down to the N.E. again. The difference on return was only 1/4 inch, or 1"-5, on 3,000 feet distance, and 900 feet height." The quote describes amazing accuracy in Petrie's mensurations at Giza. "The mean base being 9068-8 ± 0.5 inches" For all his modesty, Petrie got the mean base of G1 exactly, as judged through the prism of our authoritative geometrical model, and his mean sides for the other two pyramids are in full agreement with the CAD model, too. __________________________ Full length minus half the G3 containing box at 45 degrees long side 42982.68777595'' x short s. 13935.87257566 = 599,001,259.80 Petrie versus Cole ------------------------------------------------------- > What irks me, Jiri, is your persistent refusal to address the question of intent; you have yet to > provide any separate evidence that this pattern was created intentionally by the designers of the > Giza pyramids and temples. Whenever you reconcile the obligatory appreciation for the eternal beauty of the geometry involved, and the fact that this is Giza, the issue of intent may become clearer. Such a design certainly places the layout into the highest category of sophistication. > According to Lehner (The Complete Pyramids 1997) the base of Menkaure’s pyramid is 335 x 343 feet. > Yes, this is contrary to Petrie’s measurements (mean 346.13 x 346.13) but does this mean that Lehner is wrong? It most certainly does, considering that his figures differ wildly from not only Petrie, but also Cole, who after all did come close to Petrie in measuring the Great Pyramid. It pits him alone against two widely acknowledged professionals. plus, Lehner was caught cheating in a drama of his "This Old Man Pyramid", if I have the title right. A mechanical shovel was used to move some blocks, but no mention of the fact was made in the flick. I found that typical of the Pyramidophobia, which so torments some academicians that they will sell their soul to the devil. > > from Cole's survey report: >> "These differences in azimuth are due to the fact that the new azimuths are found from the actual directions of the sides determined from the excavated pavement, Cole took series of measurements of the available sections of the excavated pavement. The various hypothetical lines were then averaged out, and extended until they met near the corners. Considering how close Cole comes to Petrie, he did a great job! > .. a hypothetical base obtained by computing “a square that shall pass > through the points of the casing found on each side, and having also > its corners lying on the diagonals of the sockets.” a) Yes, the acclaimed anomalously accurate casing! "The quality of work," said Petrie, "equaled modern opticians, but on the scale of acres." Determination of lines from the plane of the casing blocks, and their projection down to the pavement to produce an averaged out line in the pavement should naturally be superior to relying on measurements from a single line, as Cole had done. The descending gallery shows similar accuracy in that it deviates from its axis over the course of 350 feet by a quarter inch (6 millimeters) side to side, and only one-tenth of an inch (2.5 millimeters) up and down. In using the anomalously accurate plane of the casing blocks to obtain a hypothetical line along the pavement, Petrie seems to have achieved even greater accuracy. b) Corners lying on the diagonals of the sockets: This was another logical decision by Petrie, which gave his method further advantage over Cole's. Clearly, the sockets were the target the builders were aiming the sides at. Petrie was a consummate professional. In my eyes, his drive to provide the most accurate data on Giza surpassed Cole's. After all, Cole could only be bothered to survey one pyramid. Thus he forfeited further experience with measuring at Giza, which might have given him a little more insight. The fact that Petrie's measurements set the position up for an incredibly accurate regeneration from a clean slate, using the noble Golden Section, can by no means be discounted. With this reconstruction of the Giza-layout everything clicks into place. A click in the reconstruction - a booming cannon shot across the bow of orthodox Egyptoloogy! Petrie's brilliant achievement: Although academic opinions suggest that measurements of the Great Pyramid by Cole supersede those by Petrie, I am confident in the belief that Petrie did a better job than Cole by the virtue of choosing the better method for the circumstances. I believe in what is perfect through the prism of my own experience. G2 It is noteworthy because it gets some things right. Legon starts out with a key assumption. After observing that the total North to South distance for the pyramids rounds out to 1732 Royal Cubits (determined by Petrie from his study of the Great Pyramid), he assumes that this was the intended value, because it gives the first four digits of the square root of 3. This correct assumption enables him to carry on and provide a solid proof for it, as axial spaces between the pyramids exhibit group behavior in approximating the square roots of 2, 3,5, and 7. Legon's study is also impressively accurate for the positions of the east and west sides of the Second Pyramid, and the west side of the Third Pyramid. In other cases it cannot be deemed accurate, however. Its shortcoming is one sided focus on numbers at the expense of geometry. Overall, Legon's interpretation puts the ancient builders on a level most expect - they had a simple plan, and executed it really well, albeit somewhat unevenly. For this reason, I find it hard to grasp, why Legon's theory does not command more attention from the mainstream. His only sin is making plain the Egyptian knowledge of square roots to several digits, whereas the mainstream scoffs at any idea of a unified plan whatsoever. While our reconstruction inherits Legon's basic idea (1732 cubits), it gives the Giza creators a lot more credit for technical prowess by having them intend this distance as the far more precise 1,732.05 cubits. Due to this upgrade the cubit system then starts shining brightly. Overall, this is a case of reality surpassing Sci-Fi. It is self evident that the workshop from which the trilogy came could only belong to a powerful and highly advanced agency with a global reach. |
| Next - The Layout of Giza's Pyramids is a minimum of 15,000 years old | |
| Testing the Nazca Monkey for Connections to the Great Pyramid | |
|
|
| Index Page | |
| Atlantean Message in Numbers - The Frame | |
| The Frame - the Hex-Machine - a family of three hexagons | |
| The Abydos Helicopter & the Golden Section | |
| Hesire's Tomb Door | |
| Giza Pyramid Temples & the Golden Section | |
| http://www.sciencedaily.com/releases/2010/01/100107143909.htm | http://www.sciencedaily.com/releases/2009/05/090528135406.htm
|