Frame
3 - Complex
Geometry
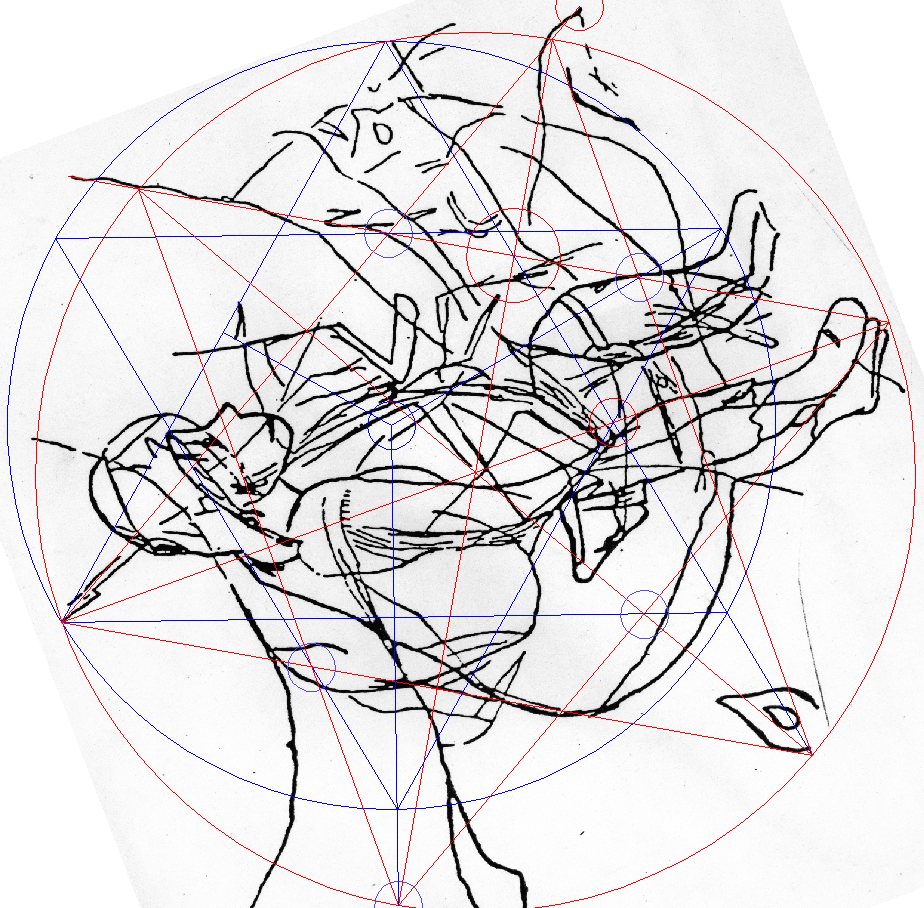
The Hex-Machine
Three generations of hexagons based on the Athena engraving's boundary points
The
Frame teaches geometry: two dynamic star systems,
so far, in which stars rise from other stars. One is an
intricate design made of three
generations of hexagonal stars. We remember the Strong Connection (B-G) and the Tri-balance (EFGH) which stole the show in the
previous chapter. Here, the same agents dominate in the hexagonal arragement below, the Big Hex. The
star shares centers with the Main Square; the fact is pretty well a
guarantee of an exact relationship between the Cone & Square
configuration and the Hex-Machine. However, I haven't yet discovered it.
Be it as it may, it's undeniable that the design has
theoretical, didactical value, for it concerns itself with some finer
points of a classical position from geometry.

a) Rounded
to the
nearest degree, The angle F-G-H measures 120 degrees.
b) The line G-B then divides F-G-H into two
60 degree angles.
c) G-B
passes through the center of the Main Square with
faultless
accuracy. In the diagram, the Square's axes are represented by
the red cross hairs within the small circle.
d) The lines connecting
the Square's center (the 0,0 point) to
'E'
and 'G' hold together a 60 degree angle. They create a close facsimile of an
equilateral triangle
with the extension of F-G, as below.

The Big Hex
So, we have some
lines and
an equilateral triangle which could all be part of
one regular
hexagon. So, why not draw it?
The result is seen in the first diagram; there is splendid
fit between the big
hexagon and
the engraving. For
instance, the hexagon's circumcircle covers the image
remarkably well. The same can be said for the envelope around the human
figure.
I
noticed the
Big Hexagon first, because it is so obvious.
Its origin remains unknown until one understands two other 60
degree angles in this position, how they work together.
Several experiments have to be carried out.
The basic array of the 60
degree angles on the Frame is as below.

Each
line from B to one of the
four
points E,F,G,H
serves as an arm of at least one
60-degree
angle (rounded out to the nearest degree). |

If we rotate E-J clock-wise
60-degrees around 'E' - it turns out that the new line can always be easily recreated
without measurement, just relying on line-guides (marked by red
arrows) supplied by the engraving. Note that the line JB doesn't
actually hit 'B'. Instead, it subtends a section of the engraving very cleanly.
Next, we complete the angle JEB into
an
equilateral triangle by resting the third side on the Frame-point 'B'
(diag. above).

The triangle's circumcircle then touches 'H' (above).
Moreover, lines from 'E' to 'H', and 'H' to 'B' also create an angle which rounds out to 60 degrees.
The
position is now an
illustration of a geometrical theorem:
Any
point on the
circumcircle
of an equilateral triangle connects to that
triangle's
corners by lines holding 60 degrees when above the basis, and
120
degrees, when below the basis.
The
point H
happens to
be just such a point. So, it must have been drawn with the red triangle already in place.
(diag. below)
It also seems that B-H was drawn from 'B', so that it would pass through 'P', a point on the Red Hexagon.
Next, complete E-H-B into an equilateral triangle set by E-H, which otherwise subtends the Tri-balance.

(Above)
Both the red and blue figures are perfectly regular, but
their coordination is slightly imperfect in illustrating a special case.
(Below) Perfecting the positional idea brings the blue figure visibly away from
the H point. Each
of the thirteen Frame points serves many masters (functions), thus, not
all can be served ideally. What matters is that exact ideas can be effectively
communicated by the language of approximations, and that's the case here.
|
A Special Case
Here is the design with more perfect points in common (circled) to the
two stars
without interference of the
engraving's
background.

|
Any changes in the position of "F" on the circumcircle eliminate most, but not all, of
the perfect common points.
Clearly, the position is more than just an example of the basic theorem; it deals with
a
special case

further refining that theorem. This special case
occurs only when
the line B-H ( or
its mirror image )
passes through the circled point
on the other figure, as in the diagram above (at 1/4
of the circle's diagonal,
1/3 of the triangle's height).
The
Hex-Machine

The
above image shows the three figures as given by the engraving: the
Red Hex, the Blue Hex, and the Big Hex. Each figure is
geometrically perfect per se but slightly off perfection in relation to
the other two at portraying exact relations found among them. This
imperfection is clearly visible at the crucial point 'B', where the
magenta-coloreddiagonal of the Big Hex should pass exactly through the point, which the other two stars have in common.
That said, one has to marvel at how the image above gives us a perfect
picture of what is going on; it is an accurate depiction of exact
ideas. Points that should be perfect exist instead in tightly confined
spaces sometimes bordering on invisibility.
|

The
Big Hexagon
is third-generation!
The first hexagon found on the Frame
- the Big
Hex and the other two hexagons coincide at various points.
Could it be that like the second hexagon is a special case of
the first hexagon, the Big Hexagon is a special case based on both?
In the diagram
above, we see how the Big Hexagon
fits together with
the orange star - the Hex Machine's first generation. The
diagram below shows the Big Hexagon and the Hex
Machine's second
generation, and their points of exact coincidence.

Take those ideas and put them together, and you get the big picture.
|
|
All three
hexagonal system
together become the Hex Machine.

It's
time again to review the
standard
argument against research like this - that one can find
some wonderful geometric order in anything -
bicycles, dimensions
of cereal
boxes, pieces of wind-blown newspaper,
etc. Here, that argument holds no water; the
Frame exemplifies a
different kind of order. It's highly intelligent, no doubt about it.
|












